Читайте также:
|
Эллипсоид
Эллипсоид (рис. 3.1) имеет каноническое уравнение 
, (3.19) где 
- полуоси. Также это уравнение можно записать в виде 
.
 |  | ||
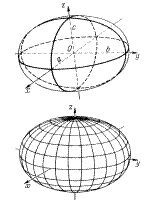Рис. 3.1. Рис. 3.2.
Если 
, то имеем сплющенный эллипсоид вращения, получающийся при вращении вокруг малой оси эллипса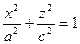 
, лежащего в плоскости Оxz. Если 
, имеем вытянутый эллипсоид вращения, который получается при вращении лежащего в плоскости Oxz, эллипса 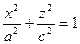вокруг его большой оси (рис. 3.2). При 
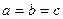имеем сферу (шар) 
.
Сечение эллипсоида любой плоскостью есть эллипс (в частном случае – круг). Объём эллипсоида равен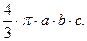 
Как уже было указано, частным случаем эллипсоида является шар или сфера, уравнение шара получается из уравнений эллипсоида при a=b=c, объём сферы равен 
.
Дата добавления: 2015-07-11; просмотров: 97 | Нарушение авторских прав