
Читайте также:
|
Чаще всего метод сечений (метод параллельных плоскостей) используют при определении формы поверхности 2-ого порядка, если поверхность задана общим уравнением (2.1) и еще не приведена к каноническому виду. Однако сам метод не зависит от уравнения, которым задана поверхность. Проиллюстрируем использование метода на примере анализа эллипсоида.
Чтобы более наглядно представить себе форму эллипсоида, заданного уравнением (3.2), выясним форму линий пересечения его плоскостями, параллельными какой-либо из координатных плоскостей. Ради определенности рассмотрим линии Lh пересечения эллипсоида с плоскостями
z = h, (3.4)
параллельными плоскости Оxу. Уравнение проекции L*h линии Lh на плоскость Оxу получается из уравнения (3.2), если положить в нем z = h. Таким образом, уравнение этой проекции имеет вид

(3.5)

Если положить
то уравнение (3.5) можно записать в виде
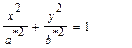
(3.6)
Таким образом, выясняется, что L*h представляет собой эллипс с полуосями а * и b *, которые могут быть вычислены по формулам (3.6). Так как Lh получается «подъемом» L*h на высоту h по оси Оz (см. (3.4)), то и Lh представляет собой эллипс.
Представление об эллипсоиде можно получить следующим образом.
Рассмотрим на плоскости Оxу семейство эллипсов (3.6) (рис. 3.12), полуоси а* и b* которых зависят от h, и каждый такой эллипс снабдим отметкой h, указывающей, на какую высоту по оси Оz должен быть «поднят» этот эллипс.

Рис. 3.12.
Метод сечений позволилполучить своего рода «карту» эллипсоида при виде на него «сверху».
Используя такие «карты» во всех трех координатных плоскостях, легко представить себе пространственный вид любой поверхности 2-ого порядка.
Общее уравнение и инварианты поверхности 2-ого порядка
Пусть поверхность S задана в декартовой системе координат  уравнением:
уравнением:

Если хотя бы один из коэффициентов 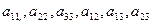 отличен от нуля, то поверхность S называют поверхностью второго порядка.
отличен от нуля, то поверхность S называют поверхностью второго порядка.
Теорема 1. Для произвольной поверхности второго порядка S существует такая декартова прямоугольная система координат  , что в этой системе поверхность S имеет уравнение одного из следующих канонических видов:
, что в этой системе поверхность S имеет уравнение одного из следующих канонических видов:
1)  - эллипсоид,
- эллипсоид,
2) 
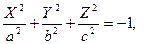 - мнимый эллипсоид,
- мнимый эллипсоид,
3) 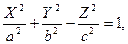 - однополостный гиперболоид,
- однополостный гиперболоид,
4) 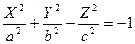 - двуполостный гиперболоид
- двуполостный гиперболоид
5)  - конус,
- конус,
6)  - мнимый конус (точка),
- мнимый конус (точка),
7) 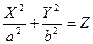 - эллиптический параболоид,
- эллиптический параболоид,
8) 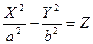 - гиперболический параболоид,
- гиперболический параболоид,
9)  - эллиптический цилиндр,
- эллиптический цилиндр,
10)  - мнимый эллиптический цилиндр,
- мнимый эллиптический цилиндр,
11)  - две мнимые пересекающиеся плоскости,
- две мнимые пересекающиеся плоскости,
12) 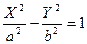 - гиперболический цилиндр,
- гиперболический цилиндр,
13) 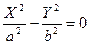 - две пересекающиеся плоскости,
- две пересекающиеся плоскости,
14) 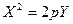 - параболический цилиндр,
- параболический цилиндр,
15) 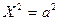 - две параллельные плоскости,
- две параллельные плоскости,
16)  - две мнимые параллельные плоскости,
- две мнимые параллельные плоскости,
17) 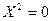 - две совпадающие плоскости.
- две совпадающие плоскости.
В этих уравнениях  - положительные параметры.
- положительные параметры.
Функция  называется квадратичной формой, соответствующей уравнению (3.1). Характеристическим уравнением квадратичной формы
называется квадратичной формой, соответствующей уравнению (3.1). Характеристическим уравнением квадратичной формы  называется уравнение
называется уравнение
 (3.2)
(3.2)
а корни  уравнения (3.2) называются характеристическими числами квадратичной формы
уравнения (3.2) называются характеристическими числами квадратичной формы  .
.
В общем случае характеристическое уравнение (3.2) записывается в виде
 (3.3)
(3.3)
где
 (3.4)
(3.4)  (3.5)
(3.5)
 (3.6)
(3.6)
Обозначим
 , (3.7)
, (3.7)

 (3.8)
(3.8)
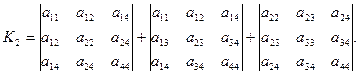 (3.9)
(3.9)
Значения 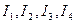 не меняются при переходе от одной декартовой прямоугольной системы координат к другой, полученной в результате поворота осей координат и переноса начала координат, то есть являются инвариантами поверхности S относительно поворота осей координат и переноса начала.
не меняются при переходе от одной декартовой прямоугольной системы координат к другой, полученной в результате поворота осей координат и переноса начала координат, то есть являются инвариантами поверхности S относительно поворота осей координат и переноса начала.
Значения  и
и  являются инвариантами поверхности S только относительно поворота осей координат
являются инвариантами поверхности S только относительно поворота осей координат
(их часто называют семиинвариантами).
Замечание 1. Для вычисления инварианта  можно использовать формулу
можно использовать формулу

Теорема 2. Для любой поверхности второго порядка S существуют углы  и числа
и числа 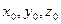 такие, что с помощью преобразования поворота осей и переноса начала координат
такие, что с помощью преобразования поворота осей и переноса начала координат
 (3.11)
(3.11)
уравнение (3.1) приводится к одному из следующих пяти видов (групп):
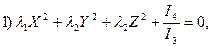 если
если  (3.12)
(3.12) 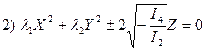 , если
, если  (3.13)
(3.13)
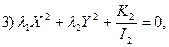 если
если 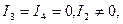 (3.14)
(3.14)
 если
если 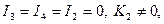 (3.15)
(3.15)
 если
если  (3.16)
(3.16)
где  - определены формулами (3.4)-(3.9) соответственно, а
- определены формулами (3.4)-(3.9) соответственно, а  - корни характеристического уравнения (3.3).
- корни характеристического уравнения (3.3).
Дата добавления: 2015-07-11; просмотров: 261 | Нарушение авторских прав