
|
Читайте также: |
Пусть: 1) в точках двусторонней гладкой (или кусочно-гладкой) поверхности s из пространства  , ограниченной кусочно-гладким контуром, определена ограниченная скалярная функция
, ограниченной кусочно-гладким контуром, определена ограниченная скалярная функция  ; 2)
; 2) 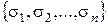 - произвольное разбиение s на n частей
- произвольное разбиение s на n частей  с площадями
с площадями  и диаметрами
и диаметрами  ; 3)
; 3) 
 - произвольный набор точек;
- произвольный набор точек;
4)  - интегральная сумма, соответствующая данному разбиению поверхности s и выбору точек
- интегральная сумма, соответствующая данному разбиению поверхности s и выбору точек  .
.
Определение. Конечный предел интегральной суммы 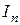 при
при 
 ,не зависящий ни от способа разбиения поверхности s, ни от выбора точек
,не зависящий ни от способа разбиения поверхности s, ни от выбора точек  , называется поверхностным интегралом первого рода от функции
, называется поверхностным интегралом первого рода от функции  по поверхности s:
по поверхности s:
 .
.
Вычисление ПИ-1. Теорема 14.10. Если: 1) поверхность s задана неявным уравнением  и
и  есть решение этого уравнения при
есть решение этого уравнения при 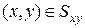 или
или  - решение уравнения при
- решение уравнения при  , или
, или  -решение уравнения при
-решение уравнения при  , где
, где  - проекции s на плоскости
- проекции s на плоскости  - соответственно, 2) между точками s и ее соответствующей проекцией установлено взаимно однозначное соответствие, то
- соответственно, 2) между точками s и ее соответствующей проекцией установлено взаимно однозначное соответствие, то

 , (6.3)
, (6.3)
причем ПИ-1 существует, если существуют соответствующие двойные интегралы.
Здесь  координаты вектора
координаты вектора  и находятся по формулам (6.1).
и находятся по формулам (6.1).
ПИ-1 не зависит от выбора стороны поверхности.
Следствие. При явном задании s:  в силу (6.2) из (6.3) получим
в силу (6.2) из (6.3) получим
 . (6.4)
. (6.4)
Некоторые приложения ПИ-1
1. Масса материальной поверхности. Пусть  - поверхностная плотность материальной поверхности s площади s. Тогда масса этой поверхности
- поверхностная плотность материальной поверхности s площади s. Тогда масса этой поверхности
 .
.
2. Площадь искривленной поверхности s. Если принять в предыдущей формуле  , то масса поверхности s числено равна площади s, т.е.
, то масса поверхности s числено равна площади s, т.е.
 .
.
3. Статические моменты материальной поверхности s с поверхностной плотностью  и массой m относительно плоскостей
и массой m относительно плоскостей  соответственно равны:
соответственно равны:  ,
,  ,
,  .
.
4. Координаты центра тяжести материальной поверхности s:
 .
.
Задания
1. Записать линейные свойства ПИ-1.
2. Записать свойство аддитивности для ПИ-1.
Пример 23. Вычислить ПИ-1  , где s - часть плоскости
, где s - часть плоскости
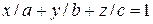 , вырезанная цилиндром
, вырезанная цилиндром 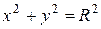 (рис.14.26).
(рис.14.26).
 |

Рис. 14.26
Ñ Поверхность s проецируется на плоскость 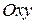 в круг
в круг  . По формуле (6.4)
. По формуле (6.4) 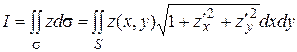 . Из уравнения s следует
. Из уравнения s следует  ,
, 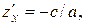

 ; тогда
; тогда 
 =
=
= 

=  .#
.#
Пример 24. Вычислить ПИ-1  , где s - полная поверхность тетраэдра, отсекаемого от первого октанта плоскостью
, где s - полная поверхность тетраэдра, отсекаемого от первого октанта плоскостью  .
.
Ñ Полная поверхность s тетраэдра складывается из его граней:  ,где
,где  (рис.14.27).
(рис.14.27).
 Выпишем уравнения поверхностей
Выпишем уравнения поверхностей  и вычислим для них элементы
и вычислим для них элементы  :
:
а)  ;
;
б) 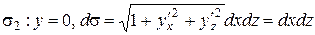 ;
;
|
 ;
;
г)  .
.
Задав уравнения поверхностей в явном виде, мы определили тем самым плоскости проецирования их;  - области, на которые проецируются
- области, на которые проецируются  .
.
 .
.
По поводу последней записи напомним, что следует в подынтегральной функции  независимые переменные (переменные из области
независимые переменные (переменные из области  ) оставлять без изменения, зависимую переменную заменить из явного уравнения соответствующей поверхности, а
) оставлять без изменения, зависимую переменную заменить из явного уравнения соответствующей поверхности, а  заменить выражением, полученным выше, причем
заменить выражением, полученным выше, причем  . Находим:
. Находим:
 ;
;
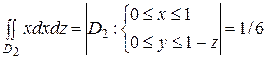 , так как области
, так как области  и
и  переходят одна в другую заменой
переходят одна в другую заменой  на
на  ;
;
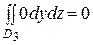 ;
; 
=  .
.
 .#
.#
Дата добавления: 2015-10-30; просмотров: 113 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Независимость КИ-2 от пути интегрирования | | | Поверхностные интегралы второго рода (ПИ-2) |