Векторных линий поля

Определение 1. Векторным полем называется часть пространства (или все пространство), в каждой точке M которого задано какое-либо физическое явление, характеризуемое векторной величиной .

Если в пространстве введена декартова прямоугольная система координат, то задание вектор - функции поля сводится к заданию трех скалярных функций:

. (1.1)

Простейшими геометрическими характеристиками векторных полей являются векторные линии и векторные трубки.

Определение 2. Векторными линиями поля называются линии (кривые), в каждой точке M которых направление касательной совпадает с направлением поля в этой точке.

Определение 3. Векторной трубкой называется поверхность, образованная векторными линиями, проходящими через точки некоторой лежащей в поле замкнутой кривой, не совпадающей (хотя бы и частично) с какой – либо векторной линией.

Если поле задано формулой (1.1), то уравнение векторных линий дается системой дифференциальных уравнений

. (1.2)

Замечание. Методы решения систем (1.2) (систем в симметрической форме) рассматриваются в теории дифференциальных уравнений.

Определение 4. Векторное поле называется плоским, если в специально подобранной системе координат оно имеет вид:

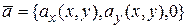(1.1¢)

Система уравнений (1.2) для таких полей имеет вид

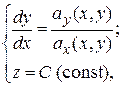(1.2¢)

и, таким образом, векторные линии плоского поля – это кривые, лежащие в плоскостях, параллельных плоскости Oxy.

Пример 1. Найти векторные поля 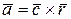(вектор =const; - радиус вектор точки ).

Решение. Пусть ; тогда

.

Составим систему дифференциальных уравнений векторных линий (1.2):

.

Эту систему решаем методом интегрируемых комбинаций. Для получения интегрируемой комбинации умножим числитель и знаменатель первой дроби на x, второй – на y, третьей – на z; сложим почленно. По свойству пропорций получим

,

откуда получаем интегрируемую комбинацию: ; интегрируя ее, получим 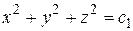- первый интеграл системы. Вторую интегрируемую комбинацию получим, умножая числитель и знаменатель первой дроби на 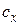, второй – на , третьей – на ; сложим почленно, получим
;

отсюда и, следовательно, .
Таким образом система уравнений определяет искомые векторные линии: это окружности, центры которых находятся на прямой, проходящей через начало координат в направлении вектора ; плоскости, в которых они лежат, перпендикулярны указанной прямой.

Пример 2. Найти векторные линии магнитного поля бесконечного проводника тока.

Решение. Считаем, что проводник направлен по оси Oz, и в этом же направлении течет ток . Вектор напряженности магнитного поля, создаваемого током, равен , где 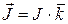- вектор тока, 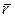- радиус вектор точки ; 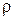- расстояние от оси проводника до точки M. Имеем, далее, , и уравнение (1.2¢) имеет вид: , , откуда - векторные линии суть окружности с центрами на оси Oz.

Дата добавления: 2015-10-30