
|
Читайте также: |
Пусть поле 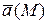 - дифференцируемое поле (то есть проекции вектора поля на оси координат являются дифференцируемыми функциями).
- дифференцируемое поле (то есть проекции вектора поля на оси координат являются дифференцируемыми функциями).
Определение. Вихрем векторного поля  (обозначается rot
(обозначается rot  ) называется вектор, проекция которого на произвольный вектор
) называется вектор, проекция которого на произвольный вектор  определяется как предел отношения циркуляции поля
определяется как предел отношения циркуляции поля  по некоторому контуру (L), содержащему точку M, и лежащему в плоскости, перпендикулярной вектору
по некоторому контуру (L), содержащему точку M, и лежащему в плоскости, перпендикулярной вектору  , к площади области, ограниченной этим контуром, при условии, что этот контур стягивается в точку M, а площадь области (S) стремится к нулю:
, к площади области, ограниченной этим контуром, при условии, что этот контур стягивается в точку M, а площадь области (S) стремится к нулю:
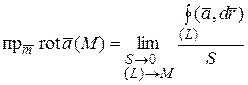 . (1.13)
. (1.13)
В трехмерном пространстве  через декартовы прямоугольные координаты вектора
через декартовы прямоугольные координаты вектора 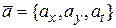 выражается следующим образом:
выражается следующим образом:
 , (1.14)
, (1.14)
или в удобной для запоминания символической форме
 . (1.15)
. (1.15)
Теорема Стокса. Пусть координаты вектора  +
+ 
 непрерывны и имеют непрерывные частные производные. Тогда циркуляция векторного поля
непрерывны и имеют непрерывные частные производные. Тогда циркуляция векторного поля  по замкнутому контуру (L) равна потоку вихрей поля через произвольную поверхность (S), натянутую на этот контур:
по замкнутому контуру (L) равна потоку вихрей поля через произвольную поверхность (S), натянутую на этот контур:
 . (1.16)
. (1.16)
Предполагается, что ориентация контура (L) и поверхности (S) согласованы: при положительном обходе контура нормаль направлена от “ног к голове”.
Свойства ротора: 1)  ; 2)
; 2)  .
.
Определение. Векторное поле  называется безвихревым в данной области (V), если
называется безвихревым в данной области (V), если  .
.
Пример 1. Найти ротор поля вектора напряженности магнитного поля  .
.
Решение.Вектор  в координатной форме:
в координатной форме: 

 . Вычислим ротор по формуле (1.15):
. Вычислим ротор по формуле (1.15):

+  -
-
- поле напряженности  - безвихревое поле.
- безвихревое поле.
Пример 2. Вычислить циркуляцию вектора 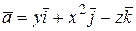 по контуру
по контуру  1)непосредственно, 2)по теореме Стокса.
1)непосредственно, 2)по теореме Стокса.
|
 Решение. 1)Контур (L) – окружность радиуса
Решение. 1)Контур (L) – окружность радиуса  , лежащая в плоскости
, лежащая в плоскости
 , так что
, так что  ,
,  . Для циркуляции вектора
. Для циркуляции вектора  имеем:
имеем:  . 2)Для вычисления циркуляции по теореме Стокса выберем какую-нибудь поверхность (S), натянутую на контур (L).Естественно в качестве (S) взять круг, имеющий линию (L) своей границей. Согласно выбранной ориентации контура нормаль
. 2)Для вычисления циркуляции по теореме Стокса выберем какую-нибудь поверхность (S), натянутую на контур (L).Естественно в качестве (S) взять круг, имеющий линию (L) своей границей. Согласно выбранной ориентации контура нормаль 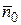 к кругу необходимо взять равной
к кругу необходимо взять равной  . Вычислим ротор:
. Вычислим ротор:  .
. 
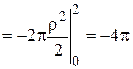 .
.Дата добавления: 2015-10-30; просмотров: 138 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Линейный интеграл вектора. Циркуляция векторного поля | | | Задачи для самостоятельного решения |