
Читайте также:
|
Перейти в тройном интеграле  к цилиндрическим координатам
к цилиндрическим координатам  или сферическим координатам
или сферическим координатам  и расставить пределы интегрирования:
и расставить пределы интегрирования:
52. V – область, находящаяся в первом октанте и ограниченная поверхностями  ,
,  .
.
53. V – область, ограниченная поверхностями 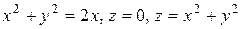 .
.
54. 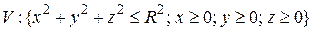 .
.
55. 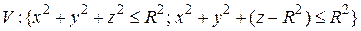 .
.
Перейдя к цилиндрическим или сферическим координатам, вычислить интегралы:
56.  . 57.
. 57. 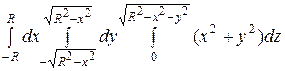 .
.
58.  . 59.
. 59.  .
.
60.  , где
, где  .
.
61.  , где
, где  .
.
62.  , где область V ограничена поверхностью
, где область V ограничена поверхностью  .
.
Некоторые приложения двойных и тройных интегралов
1. Площадь фигуры. а) Для плоской фигуры 
 . (4.1)
. (4.1)
б) Площадь части искривленной поверхности рассматривается в разделе 14.6. этой главы.
2. Объем тела V:  (
(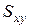 - проекция V на плоскость Oxy):
- проекция V на плоскость Oxy):
 (4.2)
(4.2)
или  . (4.3)
. (4.3)
3. Масса. а) Если  - поверхностная плотность массы плоской фигуры
- поверхностная плотность массы плоской фигуры  , то
, то
 . (4.4)
. (4.4)
б) если 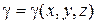 - объемная плотность массы тела
- объемная плотность массы тела  , то
, то
 . (4.5)
. (4.5)
Для однородных фигур и тел плотность  примем равной единице.
примем равной единице.
4. Статические моменты и координаты центра тяжести. а) Для плоской фигуры  c плотностью
c плотностью  и массой m статические моменты относительно координатных осей:
и массой m статические моменты относительно координатных осей:
 ,
,  ;
;
координаты центра тяжести:
 ,
,  .
.
б) Для тела V с плотностью 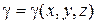 и массой m статические моменты относительно координатных плоскостей
и массой m статические моменты относительно координатных плоскостей
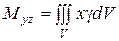 ,
,  ,
,  ;
;
координаты центра тяжести:
 ,
,  ,
,  .
.
Пример14. Найти массу пластинки 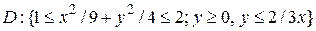 с поверхностной плотностью
с поверхностной плотностью  .
.
Ñ По формуле (4.4) 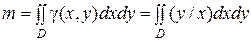 . Область D и подынтегральная функция совпадают с областью интегрирования и функцией из примера 9 в пункте 14.2.4 при
. Область D и подынтегральная функция совпадают с областью интегрирования и функцией из примера 9 в пункте 14.2.4 при  ; там же вычислен этот двойной интеграл, поэтому
; там же вычислен этот двойной интеграл, поэтому  и при
и при  . #
. #
Пример 15. Найти массу тела.  , если объемная плотность
, если объемная плотность 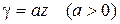 .
.
Ñ По формуле (4.5)  . Тройной интеграл I по данной области V вычислен в примере 12 из пункта 14.3.3,
. Тройной интеграл I по данной области V вычислен в примере 12 из пункта 14.3.3,  , и потому
, и потому  .#
.#
Пример 16. Найти объем тела 
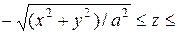
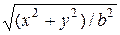 ;
; 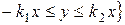 ,
, 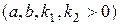 .
.
Ñ Из формулы (4.3)  . Тело V ограничено сферами, полуконусами и плоскостями (рис.14.21).
. Тело V ограничено сферами, полуконусами и плоскостями (рис.14.21).

| 
|
|
|
 Из анализа уравнений и вида поверхностей следует целесообразность перехода к сферическим координатам
Из анализа уравнений и вида поверхностей следует целесообразность перехода к сферическим координатам  по формулам:
по формулам:  ,
,  ,
,  . Поверхности, ограничивающие V, преобразуются:1)
. Поверхности, ограничивающие V, преобразуются:1)  ;
; 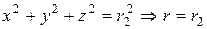 ;
;3)  или
или  ;
;
4)  ;
;
5)  ; 6)
; 6)  .
.
Область изменения сферических координат точек области V есть
 .
.
Тогда в силу формулы (3.7)  =
=
= 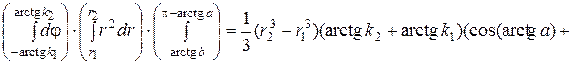
 . #
. #
Дата добавления: 2015-10-30; просмотров: 104 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Задачи для самостоятельного решения | | | Задачи для самостоятельного решения |