Способы вычисления потока

1°. Метод проектирования. Пусть поверхность (S) задана явным уравнением . В этом случае орт и . Для потока П получим формулу:

. (1.4)

Замечание 1. При проектировании на другие плоскости в подынтегральную функцию в формуле (1.4) следует добавить (множителем) проекцию на координатную ось, перпендикулярную плоскости проектирования.

В формуле (1.4) () – область на плоскости Oxy, в которую проектируется поверхность (S); произведение dxdy берется со знаком +, если угол между осью Oz и нормалью острый, и минус, если угол тупой. Символ означает, что в подынтегральную функцию вместо z надо подставить .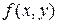

Замечание 2. Аналогичные формулы можно записать, если проектировать поверхность (S) на плоскости Oxz или Oyz.

Замечание 3. В случае неявного задания поверхности (S) вектор .

Пример 1. Найти поток векторного поля через верхнюю сторону треугольника АВС с вершинами в точках , , (см. рис.2).

Рис.2.

Решение. Составим уравнение плоскости (поверхности (S)), проходящей через три заданные точки:

,

откуда . Поверхность (S) проектируется на плоскость Oxy в область 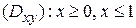, . Из условия следует, что нормаль образует острый угол с осью Oz. Имеем = ; произведение dxdy, берем со знаком “+”. Тогда по формуле (1.4)

.

Пример 2. Вычислить поля через замкнутую поверхность (S), ограниченную цилиндром и плоскостями , . Положительной стороной (по определению) считаем внешнюю сторону замкнутой поверхности.

Решение. Поверхность (S) кусочно гладкая. Разобъем ее на три части
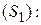(см. рис.3): . В связи с этим . 1)Для поверхности z= 0 и .

Рис.3.

Тогда . Проекция поверхности (S) на плоскость Oxy есть полукруг , . С учетом направления нормали для потока получим: . Переходя к полярным координатам, найдем 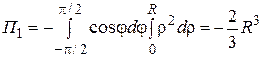.2) Для и . Поверхность проектируется на плоскость Oxy в область () (см.п.1), и поток

= .3)Для ,

и = . Однозначно поверхность проектируется на плоскость Oyz в область (), ограниченную линиями .

Исключая отсюда x, найдем проекцию этой линии на плоскость Oyz: 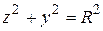. Для потока получим (напомним Замечание 1: следует учесть, что в этом случае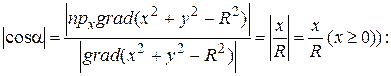

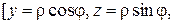
= . 4) Для потока получим .

2°. Метод проектирования на все три координатные плоскости. Пусть поверхность (S) однозначно проектируется на все три координатные плоскости: (D_xy): z = z (x, y); ; 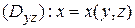.Для потока П в этом случае имеем (вторая формула из (1.3)):

(1.5)

В (1.5) знаки проекций dydz, dxdz, dxdy выбираются в соответствии с сформулированным выше правилом.

Пример 3. Найти поток вектора через часть внешней стороны сферы , заключенной в первом октанте.

Решение. Имеем . С учетом того, что поверхность расположена в первом октанте, проекции dydz, dxdz, dxdy берем со знаком “+”. По формуле (1.5) 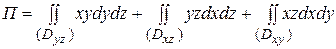. Из уравнения сферы имеем: ; ; 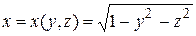и

. Очевидно, . Вычислим этот интеграл в полярной системе координат: = = = . Следовательно, .

3°. Применение формулы Гаусса-Остроградского. Приведем соответствующую теорему.

Теорема. Если в некоторой области проекции поля непрерывны и имеют непрерывные частные производные , то поток вектора через произвольную замкнутую кусочно гладкую поверхность (S), расположенную целиком в области , равен тройному интегралу от суммы по области (V), ограниченной поверхностью (S):

(1.6)

- формула Гаусса-Остроградского.

Замечание. Подынтегральная функция в тройном интеграле (1.6) называется дивергенцией (расходимостью) поля ; обозначается .

Пример 4. Вычислить поток вектора через замкнутую поверхность , .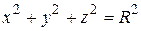

Решение. По формуле (1.6) . Для вычисления этого интеграла применим сферическую систему координат: , , ; . Таким образом,

.

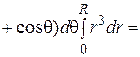
Пример 5. Используя формулу Гаусса-Остроградского (1.6), вычислить поток поля через верхнюю сторону части поверхности , расположенную над плоскостью Oxy.

Решение. Для того, чтобы можно было применить формулу (1.6), замкнем снизу данную поверхность куском плоскости Oxy, который ограничен окружностью , z = 0. Вычислим подынтегральную функцию, стоящую под знаком тройного интеграла: . Отсюда следует, что поток П =0. По свойству аддитивности , откуда искомый поток . Уравнение поверхности и . Таким образом, - поток через поверхность z =0 численно равен площади круга ; искомый поток .

Дата добавления: 2015-10-30