Алгоритм вычисления коэффициента ранговой корреляции

Условие	Решение (схема)
х (в ед.)	у (в %)	Ранги по ряду х	Ранги по ряду у	d	d^2
1,2	94,0	9,5	9,0	0,5	0,25
1,0	94,2	5,0	10,0	- 5,0	25,00
0,9	93,1	1,5	6,5	- 5,0	25,00
1,0	93,3	5,0	8,0	- 3,0	9,00
0,9	92,5	1,5	5,0	- 4,0	16,00
1,0	92,2	5,0	4,0	1,0	1,0
1,1	93,1	8,0	6,5	1,5	2,25
1,0	91,1	5,0	2,0	3,0	9,0
1,0	91,2	5,0	3,0	2,0	4,0
1,2	90,1	9,5	1,0	8,5	72,25
					d^2 =163,75

Решение. В данном случае один из рядов (ряд у) представлен показателями, выраженными в %, что соответствует качественному характеру распределения. Поэтому для определения зависимости между величиной цветного показателя и уровнем насыщения крови кислородом нужно использовать коэффициент ранговой корреляции.

При вычислении коэффициента ранговой корреляции необходимо учесть, что этот коэффициент является менее мощным критерием по сравнению с коэффициентом линейной корреляции, однако имеет более широкую область применения. Названный коэффициент корреляции используется в тех случаях, когда коррелируемые данные соответствуют количественному, качественному или порядковому распределениям.

;	где pxy - коэффициент ранговой корреляции; d - разница между рангами; n - число коррелируемых пар

Начальным этапом определения коэффициента ранговой корреляции является проведение ранжировки коррелируемых рядов (построение числовых значений рядов х и у по возрастающей или убывающей величине) путем присвоения числовым значениям каждого ряда порядковых номеров. Если числовые значения в ряду одинаковые, то их ранги будут соответствовать среднему значению порядковых мест, которые они занимают. Так в ряду х самая малая величина 0,9 (см. табл. 9.2) встречаются дважды, следовательно, для определения ее ранга необходимо сложить порядковые места и найти их среднее значение (1+2): 2 = 1,5; следующим по величине является число 1,0, которое встречается 5 раз. Это число должно занять места с 3 по 7. Для нахождения рангов необходимо: (3 + 4 + 5 + 6 + 7): 5 = 5 и т.д. Аналогично определяются ранги и для ряда у.

_;  

Найденный результат сравниваем с критическим значением оценочных таблиц (см. табл. 8, приложения). Критическое значение таблицы при n = 10 соответствует 0,64 – 0,79, следовательно, полученный показатель является статистически недостоверным; на основании имеющихся данных невозможно судить о влиянии уровня насыщения крови кислородом на величину цветного показателя (Р < 95%).

Оценку достоверности полученного коэффициента корреляции можно проводить и с использованием критерия t.

;

где

t - коэффициент достоверности; pxy - коэффициент ранговой корреляции; m - ошибка коэффициента корреляции; n - число коррелируемых пар

;

; ;

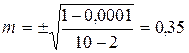Для оценки достоверности критерия t нужно определить число степеней свободы по формуле: f = n –2 = 10 – 2 = 8. Критическое значение t = 2,31 – 3,36 – 5,04 (см. табл. 1 приложения). Таким образом, второй метод оценки достоверности позволяет сделать аналогичные выводы, т.е. полученный коэффициент ранговой корреляции является статистически недостоверным. На основании имеющихся данных невозможно судить о влиянии уровня насыщения крови кислородом на величину цветного показателя (Р < 95%).

Пример 3. Определить коэффициент регрессии веса по росту для девятилетних мальчиков, если известно, что среднеквадратическое отклонение по весу (σ_х) = 2,1 кг, по росту (σ_у) = 5,6 см, коэффициент корреляции r_xy = 0,8.

Решение.

Вывод. С увеличением роста на 1 см вес мальчиков девятилетнего возраста увеличивается на 0,3 кг.

Варианты задания по теме «Корреляция»

Задание 1. На основании данных табл. 9.4 требуется определить зависимость естественного прироста населения от количества умерших по пятнадцати районам (варианты 1-15).

Задание 2. При изучении заболеваемости с временной утратой трудоспособности по пятнадцати однотипным производственным объединениям (варианты 1-15) были получены следующие стандартизованные показатели заболеваемости с временной нетрудоспособностью (см. табл. 9.5). Требуется определить: влияют ли условия труда цехов на уровень названной заболеваемости.

Задание 3. На основании данных о физическом развитии 15 групп (варианты 1-15) семнадцатилетних юношей (табл. 9.6) вычислить коэффициенты регрессии и сделать выводы.

Задания для педиатрического факультета.

1.1. На основании данных табл. 9.7 и 9.8. определить связь между уровнями рождаемости и детской смертности по пятнадцати районам (варианты 1-15).

1.2. Определить, влияет ли число детей в семье на количество пропущенных рабочих дней работающими в связи с уходом за ними из-за болезни. Показатели определены на 15 заводах (варианты 1-15) и представлены в табл. 9.9.

1.3. На основании данных о физическом развитии 15 групп (варианты 1-15) семнадцатилетних юношей (табл. 9.6) вычислить коэффициент регрессии и сделать выводы.

ТЕМА X.

Дата добавления: 2015-10-30