Оценка достоверности средних величин и различий между ними

Цель занятия: изучение методических основ оценки достоверности средних величин и различий между ними

ПЛАН ЗАНЯТИЯ

I. Рассмотрение теоретических основ оценки достоверности средних величин и различий между ними:

5. Оценка достоверности средних величин.

6. Определение доверительных границ средних величин.

7. Определение необходимого объема наблюдений.

8. Определение различий между средними величинами.

II. Оценка достоверности средних величин и различий между ними.

Порядок оценки достоверности средних величин (образец)

Пример 1. После определения средней величины (М = 58,7 см), среднеквадратического отклонения (s =± 1,8 см) и ошибки средней величины (m = ± 0,3 см) (см. табл. 4.2) необходимо провести:

1. Оценку достоверности полученных результатов с использованием формулы:

,	где M - средняя величина; m - ошибка средней величины; t - коэффициент достоверности.

Среднюю величину следует считать статистически достоверной, если коэффициент достоверности будет превышать стандартное значение оценочной таблицы 1 (см. приложение).

.

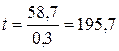Для определения стандартного значения необходимо найти число степеней свободы по формуле:

,	где f - число степеней свободы, n - число наблюдений.

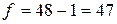
Коэффициент t = 195,7 превышает стандартные значения 1,98 (р < 0,05); 2,62 (р < 0,01) и 3,37 (р < 0,001).

Следовательно, найденная средняя величина окружности грудной клетки у девятилетних мальчиков является статистически достоверной более чем в 99,9% (р < 0,001).

2. Определение доверительных границ средней величины следует проводить по формуле:

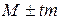,	где M - средняя величина; t - доверительный коэффициент; m - ошибка показателя.

Если t = 1, то с вероятностью в 68,3% результаты выборочного исследования могут быть перенесены на генеральную совокупность; при t = 2 вероятность переноса результатов выборочного исследования на генеральную совокупность возрастает до 95,5% и при t = 3 – до 99,7%.

В рассмотренном примере средняя величина = 58,7 см, ее ошибка соответствует ± 0,3 см.

Для обозначения доверительных границ средней величины приемлема следующая запись: 58,7 ± 0,3 см.

Предельная ошибка выборочного исследования 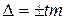позволяет определить величину доверительного интервала, в пределах которого с определенной вероятностью находится подлинная средняя величина генеральной совокупности.

3. Оценка достоверности средних величин выборочной совокупности должна проводиться на достаточном объеме наблюдений.

Необходимое число наблюдений для выборочного исследования можно определить при помощи преобразования вышеприведенной формулы предельной ошибки выборки ():

,

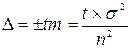где:	t - доверительный коэффициент, m - ошибка средней арифметической, σ - среднеквадратическое отклонение n - число наблюдений.

Решая приведенное равенство относительно n, получим формулу для определения необходимого числа наблюдений:

.

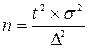Используя данные таблицы 4.2 и вычисленные на их основании показатели, проведем проверку достаточности объема наблюдений выборочной совокупности.

t – доверительный коэффициент при 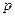= 95,5% равен 2

σ - составила ± 1,8 см

= 0,5 см (задает сам исследователь)

Следовательно, необходимый объем наблюдений выборочной совокупности равен 52.

Дата добавления: 2015-10-30