Алгоритм определения средней величины, среднеквадратического отклонения и ошибки средней величины

V (в см)	P	V х р	d = (V-M)	d^2	d^2х p
			- 3,69	13,62	27,24
			- 2,69	7,23	36,15
			- 1,69	2,86	17,16
			- 0,69	0,48	3,84
			0,31	0,10	1,00
			1,31	1,72	15,48
			2,31	5,34	26,70
			3,31	10,96	32,88

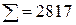
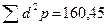
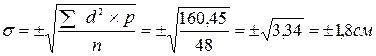
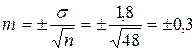
II. Порядок оценки типичности числовых значений вариационного ряда, т.е. определения принадлежности крайних вариант к совокупности по критерию τ.

В случае, если объем наблюдений меньше 30, применяются формулы:

; ;

где:	τmin - критерий для оценки принадлежности минимальной варианты;
	τmаx - для оценки принадлежности максимальной варианты;
	Vmаx - максимальная по величине варианта;
	Vmin - минимальная по величине варианта;
	Vmаx-1 - предпоследняя по величине варианта;
	V2 – вторая по величине варианта в вариационном ряду.

Согласно H₀ предполагаем, что максимальная и минимальная варианты относятся (типичны) к данной совокупности (см. пример 1, табл. 4.1).

;

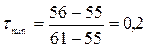После вычисления τ_min, полученный результат сопоставляется с критическим значением оценочных таблиц (см. приложение, таблица 3).

Н₀ принимается при τ < τ 0,05 и отвергается при τ > τ 0,01

При n = 8 τ _0,05 = 0,554; τ _0,01 = 0,683

τ = 0,2< 0,554 < 0,683

Следовательно, H₀ принимается τ < τ _0,05

Таким образом, числовые значения (варианты) 55 и 62 типичны для данной совокупности.

Для определения характера распределения вычисляют коэффициент ассиметрии Аs или эксцесса Еs _.

,

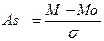где

M - средняя величина; Mo - мода вариационного ряда; s - среднеквадратическое отклонение.

Для вычисления As использованы данные примера 2.

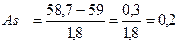
Заключение. Достоверность Аs оценить невозможно в силу малого объема наблюдений (минимальный объем наблюдений должен быть равен 25) (см. приложение, табл. 4).

Для оценки типичности числовых значений вариационного ряда (определения принадлежности крайних вариант к совокупности) в случае, если объем наблюдений больше 30, применяются формулы:

; ;

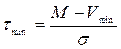где:	мax - критерий оценки принадлежности максимальной варианты к совокупности;
	мin - критерий оценки принадлежности минимальной варианты к совокупности;
	Vmax - максимальная по величине варианта;
	Vmin - минимальная по величине варианта;
	M - средняя величина;
	s - среднеквадратическое отклонение.

Согласно H₀ предполагаем, что максимальная и минимальная варианты относятся к изучаемой совокупности (см. пример 2, табл. 4.2).

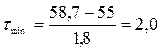
После вычисления τ, полученный результат сопоставляется с критическим значением оценочных таблиц (см. приложение, таблица 5).

Н₀ принимается при τ < τ _0,05 и

Н₀ отвергается при τ > τ _0,01

При n = 48 τ _0,05 = 0,533; τ _0,01 = 0,787

τ > чем τ _0,01 и > τ _0,05

т.е. τ_max = 1,8 > 0,787 > 0,533

τ_min = 2,0 > 0,787 > 0,533

Следовательно Н₀ отвергается. Таким образом, числовые значения 55 и 62 являются нетипичными для данной совокупности.

Для определения характера распределения коэффициент ассиметрии или эксцесса вычисляется по вышеизложенной методике (см. стр. 23).

ТЕМА V.

Дата добавления: 2015-10-30