Анализ динамического ряда

1. Определение абсолютного прироста (разность последующего и предыдущего уровней):

для 1900 года 1150 – 1110 = 40

для 1991 года 1165 – 1150 = 15

для 1992 года 1170 – 1169 = 1 и т. д.

2. Вычисление темпа прироста (процентное отношение абсолютного прироста к предыдущему уровню):

для 1990 г. 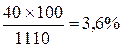для 1991 г.

для 1993 г. и т.д.

3. Нахождение темпа роста (процентное отношение последующего уровня к предыдущему):

для 1990 г. 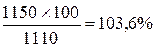для 1991 г.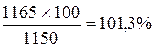

для 1993 г. 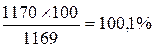и т.д.

4. Определение одного процента прироста (отношение абсолютного прироста к темпу прироста):

для 1991 г. 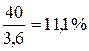для 1992 г. 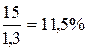и т.д.

Преобразование динамического ряда

1. Укрупнение интервалов

1110 + 1150 + 1165 +1169 + 1170 = 5764

1165 + 1150 + 1180 + 1175 + 1154 = 5824 и т.д.

2. Вычисление групповой средней

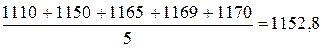
и т.д.

3. Вычисление скользящей средней:

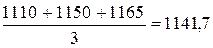
и т.д.

4. Выравнивание по способу наименьших квадратов.

При помощи названного способа находят линию, которая максимально приближается к эмпирическим данным и характеризует направление изучаемого процесса, при этом сумма квадратов отклонений фактических данных от выравненных будет наименьшей.

Для выравнивания динамического ряда используется уравнение:

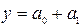
где у – величина явления, изменяющегося с течением времени;

а₀ – начальный уровень;

а₁ – начальная скорость ряда;

х – периоды времени;

n – число наблюдений.

Метод наименьших квадратов основан на упрощенном подборе способа отсчета времени х так, чтобы ∑ х = 0. Вычисление а₀ и а₁ проводят по формулам:

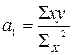
Алгоритм выравнивания данных

Годы	Число родившихся	Условное время х	ху	х^2	Выравненные данные ух
		- 7	- 7770		1154,4
		- 6	- 6900		1154,6
		- 5	- 5825		1154,8
		- 4	- 4676		1155,0
		- 3	- 3510		1155,2
		- 2	- 2330		1155,3
		- 1	- 1150		1155,2
					1155,7
					1155,9
					1156,1
					1156,2
					1156,4
					1156,6
					1156,8
					1157,0
	у = 17335	х = 0	ху = 50	х^2= 280

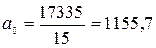
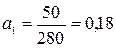
у = 1155,7 + 0,18 х (-7) = 1154,4

у = 1155,7 + 0,18 х (-6) = 1154,6

у = 1155,7 + 0,18 х (-5) = 1154,8

у = 1155,7 + 0,18 х (-4) = 1155,0

Для большей наглядности полученные данные целесообразно изобразить графически.

Варианты задания по теме «Динамические ряды»

На основании данных таблицы 8.2 (варианты 1-15) требуется провести анализ и преобразование динамических рядов путем укрупнения интервалов, вычисления групповой и скользящей средних, выравнивания методом наименьших квадратов с последующим графическим изображением данных.

ТЕМА IX.

КОРРЕЛЯЦИЯ

Цель занятия: изучение методических основ вычисления и применения коэффициентов корреляции

ПЛАН ЗАНЯТИЯ

I. Рассмотрение теоретических основ вычисления и использования коэффициентов корреляции.

1. Виды связей между явлениями.

2. Характеристика силы и направления связи при корреляционной зависимости.

3. Методика вычисления, область применения и оценка достоверности коэффициента линейной корреляции.

4. Методика вычисления, область применения и оценка достоверности коэффициента ранговой корреляции.

5. Коэффициент ассоциации, методика вычисления и оценка его достоверности.

6. Коэффициент регрессии, область применения, методика вычисления и оценка его достоверности.

II. Вычисление коэффициентов корреляции, оценка их достоверности.

Порядок определения и оценки коэффициентов корреляции (образец)

Пример 1. На основе данных таблицы 9.1 требуется определить зависимость цветного показателя крови (ряд х) от величины эритроцитов (ряд у).

Решение. В данном случае числовые значения коррелируемых рядов соответствуют количественному распределению. Поэтому для определения наличия связи между изучаемыми явлениями целесообразно вычислять коэффициент линейной корреляции.

При вычислении коэффициента линейной корреляции необходимо помнить, что названный коэффициент является более мощным по сравнению с коэффициентом ранговой корреляции, однако область его применения ограничивается количественным распределением.

Таблица 9.1

Дата добавления: 2015-10-30