
Читайте также:
|
Найти векторные линии плоских векторных полей:
1.  ; 2.
; 2.  ; 3.
; 3. 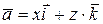 ; 4.
; 4. 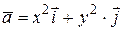 ;
;
5.  .
.
Найти векторные линии:
6. 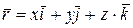 ; 7.
; 7.  , где
, где  ;
;
8.  ; 9.
; 9. 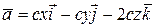 ,
,  ;
;
10.  ; 11.
; 11. 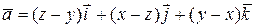 ; 12.
; 12.  ;
;
13. 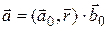 , где
, где  -постоянные векторы.
-постоянные векторы.
Найти векторные линии, проходящие через заданную точку:
14.  ,
,  ; 15.
; 15.  ,
, 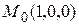 .
.
Вычислить поток векторного поля, используя поверхностный интеграл первого рода:
16.  , (S): верхняя сторона треугольника, ограниченного плоскостями
, (S): верхняя сторона треугольника, ограниченного плоскостями  ,
,  .
.
17.  , (S): внешняя сторона параболоида
, (S): внешняя сторона параболоида  , ограниченного плоскостью
, ограниченного плоскостью  ;
;
18.  ,
,  : боковая поверхность кругового цилиндра
: боковая поверхность кругового цилиндра  , ограниченного плоскостями
, ограниченного плоскостями 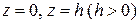 ;
;
19.  , (S): внешняя сторона части параболоида
, (S): внешняя сторона части параболоида  , расположенной в первом октанте;
, расположенной в первом октанте;
20.  , (S): полная поверхность конуса
, (S): полная поверхность конуса  , ограниченного плоскостью
, ограниченного плоскостью  ;
;
21.  , (S): замкнутая поверхность, ограниченная параболоидом
, (S): замкнутая поверхность, ограниченная параболоидом 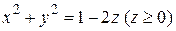 и плоскостью z = 0;
и плоскостью z = 0;
22. 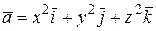 , (S): полная поверхность пирамиды, ограниченной плоскостями
, (S): полная поверхность пирамиды, ограниченной плоскостями  ,
,  ,
,  ,
,  ;
;
23.  , (S): сфера
, (S): сфера  .
.
Вычислить поток, используя метод проектирования на все три координатные плоскости.
24.  , (S): верхняя сторона круга, вырезанного конусом
, (S): верхняя сторона круга, вырезанного конусом  на плоскости
на плоскости 
25.  , (S): верхняя сторона треугольника, полученного пересечением плоскости
, (S): верхняя сторона треугольника, полученного пересечением плоскости  с координатными плоскостями;
с координатными плоскостями;
26.  , (S): часть плоскости
, (S): часть плоскости  , ограниченная окружностью
, ограниченная окружностью  , в направлении орта
, в направлении орта 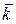 .
.
Определить поток поля, используя формулу Гаусса-Остроградского:
27.  , (S): произвольная кусочно гладкая замкнутая поверхность;
, (S): произвольная кусочно гладкая замкнутая поверхность;
28. 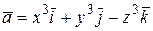 , (S): поверхность куба
, (S): поверхность куба  ,
,  ,
,  ;
;
29.  , (S): сфера
, (S): сфера  ;
;
30.  , (S): часть параболоида
, (S): часть параболоида 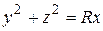 , отсекаемая плоскостью
, отсекаемая плоскостью 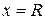 ; в отрицательную сторону оси Ox;
; в отрицательную сторону оси Ox;
31.  , (S): поверхность тела
, (S): поверхность тела  ,
,  ,
,  ,
,
 ;
;
32.  , (S): поверхность тела
, (S): поверхность тела  ,
, 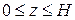 ;
;
33.  , (S):
, (S):  ;
;
34.  ;
;
35.  .
.
Найти линейный интеграл вектора на плоскости:
36.  верхняя половина эллипса
верхняя половина эллипса  от точки A (a,0), до точки B (- a,0);
от точки A (a,0), до точки B (- a,0);
37.  а) отрезок прямой OB; б) дуга параболы
а) отрезок прямой OB; б) дуга параболы  ; в) дуга параболы
; в) дуга параболы  ; г) ломаная OAB, где A (1,0); д) ломаная OCB, где C (0,1);
; г) ломаная OAB, где A (1,0); д) ломаная OCB, где C (0,1);
38. 
39.  от точки (-1, 1) до точки (2, 2).
от точки (-1, 1) до точки (2, 2).
Вычислить линейный интеграл:
40. 
41.  ,
, 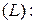 отрезок прямой от точки (1,1,1) до точки (4,4,4);
отрезок прямой от точки (1,1,1) до точки (4,4,4);
42. 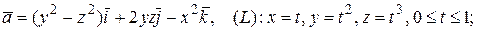
43. 
44. 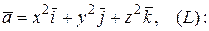 отрезок прямой от точки (0,0,0) до точки (1,1,1).
отрезок прямой от точки (0,0,0) до точки (1,1,1).
45. Дана напряженность  силового поля. Найти работу поля при перемещении массы m вдоль одного витка винтовой линии
силового поля. Найти работу поля при перемещении массы m вдоль одного витка винтовой линии 
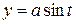 ,
,  из точки
из точки  в точку B (t =2p);
в точку B (t =2p);
46. Силовое поле образовано силой, равной по величине расстоянию от начала координат до точки ее приложения и направленной к началу координат. Найти работу поля по перемещению единицы массы вдоль дуги параболы  от точки с абсциссой
от точки с абсциссой  до точки с абсциссой
до точки с абсциссой  .
.
В задачах 47- 51 найти циркуляцию поля:
47.  в отрицательном направлении;
в отрицательном направлении;
48.  замкнутая линия, образованная отрезками осей координат Ox и Oy и другой астроиды
замкнутая линия, образованная отрезками осей координат Ox и Oy и другой астроиды  ,
,  , лежащей в первом квадранте;
, лежащей в первом квадранте;
49. 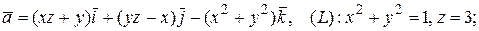
50. 
51.  линия пересечения параболоида
линия пересечения параболоида  с координатными плоскостями (в первом октанте);
с координатными плоскостями (в первом октанте);
52. Твердое тело вращается с постоянной угловой скоростью  вокруг оси Oz. Вычислить циркуляцию поля линейных скоростей вдоль окружности радиуса R, центр которой лежит на оси вращения, если плоскость окружности перпендикулярна оси вращения (циркуляция рассматривается в направлении вращения).
вокруг оси Oz. Вычислить циркуляцию поля линейных скоростей вдоль окружности радиуса R, центр которой лежит на оси вращения, если плоскость окружности перпендикулярна оси вращения (циркуляция рассматривается в направлении вращения).
53. Найти работу поля  при перемещении точки единичной массы вдоль замкнутой линии, состоящей из трех прямолинейных отрезков, лежащих в координатных плоскостях, отсекающих на осях координат отрезки, равные единице.
при перемещении точки единичной массы вдоль замкнутой линии, состоящей из трех прямолинейных отрезков, лежащих в координатных плоскостях, отсекающих на осях координат отрезки, равные единице.
Найти дивергенцию нижеследующих полей:
54.  . При какой функции
. При какой функции  будет
будет  ?
?
55.  ; 56.
; 56.  - линейная скорость точек вращающейся жидкости
- линейная скорость точек вращающейся жидкости  - угловая скорость);
- угловая скорость);
57.  напряженность магнитного поля, J,
напряженность магнитного поля, J, 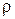 – постоянные;
– постоянные;
58.  ; 59.
; 59.  ;
;
60. Вычислить  в точке (1,-1,1).
в точке (1,-1,1).
Найти поток векторного поля через указанные замкнутые поверхности: 1) непосредственно, 2) по теореме Гаусса-Остроградского в векторной формулировке:
61. 
62. 
63. 
64. 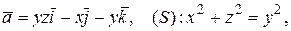
 ;
;
65. 
66. 
67. 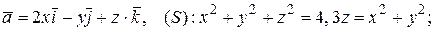
68. 
69. 
70. 
71. 
72. 
В задачах 73 и 74 вычислить ротор указанных векторных полей:
73.  74.
74. 
75. Показать, что если координаты вектора  имеют непрерывные частные производные второго порядка, то
имеют непрерывные частные производные второго порядка, то  .
.
76. Показать, что если  и
и  - постоянные векторы, то
- постоянные векторы, то  .
.
77. Показать, что  .
.
78. Показать, что  .
.
79. Показать, что векторное поле  является безвихревым.
является безвихревым.
80. Показать, что ротор поля линейных скоростей  точек вращающегося твердого тела есть постоянный вектор, направленный параллельно оси вращения, модуль которого равен удвоенной угловой скорости вращения:
точек вращающегося твердого тела есть постоянный вектор, направленный параллельно оси вращения, модуль которого равен удвоенной угловой скорости вращения:  .
.
81. Какова должна быть функция  , чтобы ротор векторного поля
, чтобы ротор векторного поля  совпадал с вектором
совпадал с вектором  ?
?
Найти циркуляцию поля по указанным контурам 1)непосредственно, 2)по теореме Стокса в векторной формулировке:
82. 
83. 
84. 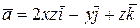 по контуру, образованному пересечением плоскости
по контуру, образованному пересечением плоскости  с координатными плоскостями;
с координатными плоскостями;
85. 
86. 
87. 
88. 
89. 
90. 
Дата добавления: 2015-10-30; просмотров: 85 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Ротор (вихрь) векторного поля | | | Частные случаи векторных полей. Операции второго порядка |