Частные случаи векторных полей. Операции второго порядка

Потенциальное векторное поле

Определение. Векторное поле называется потенциальным полем, если существует некоторая скалярная функция , градиент которой образует это поле:

. (2.1)

Функция u называется потенциалом векторного поля .

Теорема. Для того, чтобы поле было потенциальным, необходимо и достаточно, чтобы оно было безвихревым:

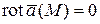. (2.2)

Формула (2.2) есть критерий потенциальности векторного поля .

Свойства потенциальных полей.

1) в области непрерывности потенциала поля u линейный интеграл не зависит от пути интегрирования и равняется приращению потенциала

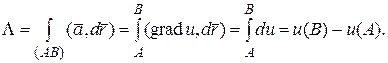(2.3)

2) циркуляция (1.9) вектора по любому замкнутому контуру, целиком лежащему в области непрерывности поля, равна нулю:

. (2.4)

3) потенциал 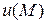находится по формуле (2.3):

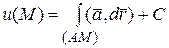, (2.5)

где (AM) – произвольная кривая, стягивающая точки A и M. Если путь (AM) взять в виде ломаной, состоящей из отрезков, параллельных осям координат (количество таких ломаных равно шести), то для нахождения потенциала может быть применена одна из формул, выражающая потенциал 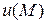через определенные интегралы ; ):

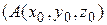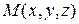. (2.6)

Пример. Проверить, что поле вектора 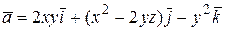является потенциальным и найти его потенциал.

Решение. Составим для данного поля критерий потенциальности (2.2):

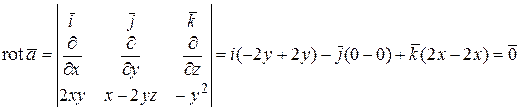
- поле потенциально. Найдем потенциал 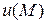по формуле (2.6): за начальную точку удобно взять точку A (0,0,0): .

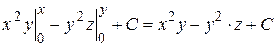Соленоидальное векторное поле

Определение. Векторное поле называется соленоидальным (трубчатым) полем, если дивергенция его равна нулю:

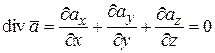(2.7)

(то есть это поле без источников и стоков). Из теоремы (1.11) следует, что в соленоидальном поле поток

(2.8)

через любую замкнутую поверхность, лежащую в этом поле.

Пример. Какие из нижеследующих полей являются соленоидальными (в естественной области определения):

1) ;

2) ?

Решение. 1) вычислим критерий (2.7): 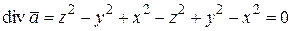- - поле вектора соленоидально; 2) - поле не соленоидально.

Дифференциальные операции второго порядка.

Дата добавления: 2015-10-30