Уравнение множественной регрессии

Подход к оценке качества спецификации уравнения множественной линейной регрессии остается таким же, как и в случае уравнения парной регрессии. В качестве меры влияния выбранных регрессоров используется коэффициент детерминации и Fтест как критерий принятия решения о качестве спецификации. Однако, в этом случае имеют место некоторые особенности.

Замечено, что с ростом числа регрессоров в модели, значение коэффициента детерминации так же возрастает. Это обстоятельство приводит к недоразумениям при анализе качества спецификации модели. Вы добавили в модель еще один регрессор, увидели, что коэффициент детерминации увеличился, кажется, что добавление регрессора положительным образом сказалось на качестве спецификации, а, на самом деле, это эффект увеличения числа регрессоров.

Чтобы нивелировать эффект влияния числа регрессоров при анализе линейных моделей множественной регрессии рассматривается модифицированный коэффициент детерминации, который связан с классическим коэффициентом детерминации следующим соотношением:

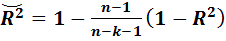(3.13)

где: 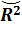- модифицированный коэффициент детерминации;

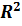– классический коэффициент детерминации;

n - объем выборки;

k - количество регрессоров в модели.

Из соотношения (3.13) видно, что при k=1 значения модифицированного и классического коэффициентов детерминации совпадают. С ростом k модифицированный коэффициент детерминации становится меньше классического.

Замечание. Функция «ЛИНЕЙН» вычисляет значение модифицированного коэффициента детерминации.

Вторая особенность связана с интерпретацией результата. Если значение 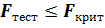, то вывод однозначный: все выбранные для моделирования регрессоры не влияют на формирование значения эндогенной переменной. А, если это условие не выполняется, то ответ – не все выбранные регрессоры не влияют на формирование значения эндогенной переменной. Это, в свою очередь, означает, что среди регрессоров могут быть, как влияющие на эндогенную переменную, так и не влияющие. Например, в модели присутствуют 10 регрессоров, условие качества выполнено, но среди них 4 регрессора «вытягивают» коэффициент детерминации, остальные 6 на нем не сказываются.

Отсюда задача, как среди регрессоров выделить те, которые оказывают влияние на значение эндогенной переменной, от тех, которые такого влияния не оказывают.

Идея решения этой задачи проста.

Пусть имеем уравнение множественной регрессии в виде:

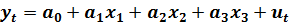(3.14)

Если, например, в этой модели регрессор 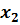не влияет на формирование значения переменной 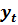, то признаком этого может быть равенство нулю параметра 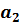при регрессоре 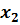. Ели параметр 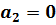, то при любых значениях регрессора 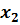произведение всегда будет равно нулю, а следовательно, этот регрессор не будет сказываться на значении эндогенной переменной.

Таким образом, для ответа на вопрос влияет или нет регрессор на формирование значения эндогенной переменной, достаточно проверить гипотезу о равенстве нулю параметра при нем.

Для тестирования гипотезы 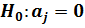создается случайная переменная в виде дроби Стьюдента:

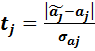(3.15)

Здесь: – значение, на равенство которому, тестируется параметр a_j, (в данном тесте );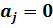

– МНК-оценка параметра ;

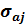– ошибка оценки параметра.

Знаем, что дробь (3.15) подчиняется закону распределения Стьюдента, следовательно, для нее можно, при заданной доверительной вероятности, найти критическое значение для принятия выдвинутой гипотезы 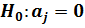. Если 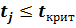, то значение параметра с номером j принимается равным нулю.

Такую проверку называют «оценкой значимости коэффициентов регрессии».

Приведенный способ применения критерия Стюдента для оценки статистических гипотез, в частности, гипотезы 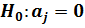, часто называют точечным методом проверки статистической гипотезы. На практике пользуется популярностью интервальный метод. Решив неравенство:

(3.16)

Относительно , получим:

(3.17)

- называют нижней границей доверительного интервала;

называют верхней границей доверительного интервала.

Если доверительный интервал «накрывает» тестируемое значение параметра, то выдвинутая статистическая гипотеза принимается. В данном тесте проверяется гипотеза 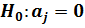, следовательно, если интервал (3.17) «накрывает» ноль, то гипотеза принимается.

Пример. Оценить модель зависимости объема продаж 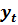от числа рекламных сообщений x₁, индекса цен на продукцию x₂, индекса цен на рекламу x₃ и протестировать качество спецификации.

Согласно заданию спецификация модели должна иметь вид:

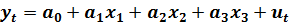(3.18)

Исходные данные для оценки модели (3.18) и результаты оценки приведены на рис. 3.4. Рис.3.4 представляет собой фрагмент листа приложения EXCEL. Там же приведены результаты обработки этих данных с помощью функции «ЛИНЕЙН» и результат анализа модели на качество спецификации.

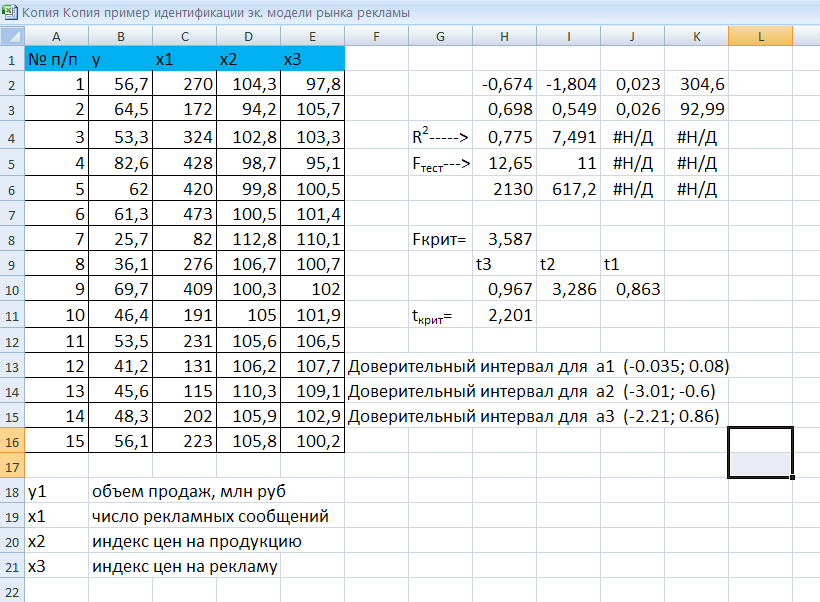
Рис. 3.4. Фрагмент листа приложения EXCEL.

Из рис.3.4 видно, что модифицированный коэффициент детерминации

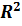=0.775, при этом значение , .

Отсюда следует, что спецификация модели (3.16) не является абсолютно плохой. Это означает, что в сумме все использованные экзогенные переменные оказывают влияние на формирование значения объема продаж ().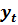

Для оценки степени влияния каждого из факторов (регрессоров) в отдельности проведен анализ значимости параметров, стоящих при регрессорах. Вычислены значения дроби Стьюдента для параметров, стоящих при регрессорах (t₁, t₂, t₃) и критическое значение дроби Стьюдента 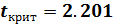. Сравнив попарно эти значения, делаем вывод, что только регрессор x₂ – индекс цен на продукцию оказывает значимое влияние на формирование объема продаж.

Влияние остальных факторов оказалось статистически незначимым и как следствие их можно удалить из спецификации модели.

К аналогичному выводу можно придти и с помощью анализа качества спецификации через доверительные интервалы. Из рис. 3.4 видно, что доверительные интервалы для параметров a₁ и a₂ накрывают ноль и, следовательно, значения этих параметров с доверительной вероятностью P_дов=0.95 можно считать равными нулю.

Другими словами, объем продаж 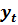зависит только от индекса цен на продукцию 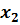. Для моделирования зависимости объема продаж достаточно ограничится спецификацией:

(3.19)

Для спецификации модели (3.19) формируется выборка результатов наблюдений. Она состоит из двух столбцов: y и x₂, вновь производится идентификация модели и проверяется ее качество спецификации.

Оценка модели (3.17) по данным рис.3.2 следующая:

При 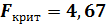модель имеет качественную спецификацию. Дополнительное тестирование модели (3.19) с помощью теста Стьюдента не имеет смысла, т.к. в спецификации (3.19) участвует всего один регрессор.

На этом закончим обсуждение вопроса о проверке качества спецификации моделей.

---

Дата добавления: 2015-10-29