Качество спецификации модели.

Начнем анализ результата оценивания модели с ответа на вопрос, насколько качественно был выполнен первый этап построения модели, а именно, не допустили ли мы ошибку, записывая спецификацию модели. На этапе спецификации модели есть возможность допустить две ошибки:

- неправильно выбрать вид поведенческой части модели (функции регрессии);

- неправильно выбрать набор экзогенных переменных, введенных в спецификацию модели.

Действительно, при спецификации модели принято ограничение об использовании только линейных алгебраических уравнений. Но вполне может оказаться, что модель существенно нелинейная (см. производственную функцию Коба-Дугласа). Во-вторых, в результате анализа поведения экономического объекта в спецификацию введен набор экзогенных переменных, который по предположению влияет на формирование эндогенной переменной. Здесь тоже возможно появление ошибок: может оказаться, что все выбранные переменные не оказывают влияния на величину эндогенной переменной или часть из них.

Тестирование качества спецификации модели направлено на выявление факторов, не оказывающих влияния на формирование эндогенной переменной.

Начнем обсуждение проблемы с примера уравнения парной регрессии.

Имеем спецификацию модели в виде:

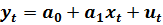(3.3)

и предполагаем, что предпосылки теоремы Гаусса-Маркова выполнены.

Тогда модель (3.3) можно записать в виде:

(3.4)

В уравнении (3.4) первое слагаемое это вклад в значение 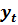влияния регрессора 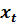, а второе - влияние случайных факторов, которые не связаны с изменениями регрессора.

Отсюда, вытекает идея тестирования. Необходимо установить, какое из слагаемых вносит наибольший вклад в общий разброс наблюдаемых значений эндогенной переменной. Характеристикой разброса случайной переменной служит дисперсия. Следовательно, необходимо определить, какое из слагаемых превалирует в функции дисперсии эндогенной переменной. Найдем дисперсию функции 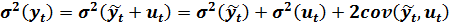(3.5):

(3.5)

Найдем значение последнего слагаемого (3.5):

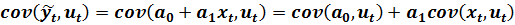(3.6)

Первое слагаемое (3.6) равно нулю т.к. ковариация между константой и случайной величиной равна нулю, второе слагаемое равно нулю в силу четвертой предпосылки теоремы Гаусса-Маркова.

В результате получаем:

(3.7)

Выражение (3.7) можно представить в виде:

(3.8)

Общая сумма квадратов (Total Sum Squares)

Введем следующие обозначения:

-

Регрессионная сумма квадратов (Regression Sum Squars)

-

Сумма квадратов ошибок (Error Sum Squares)

-

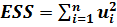Тогда выражение (3.8) можно записать как:

(3.9)

Замечание. Равенства (3.8) и (3.9) имеют место, если в модели присутствует параметр .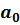

В качестве меры влияния регрессора на формирование значения эндогенной переменной y вводится коэффициент детерминации как отношение регрессионной суммы квадратов к общей сумме квадратов:

(3.10)

Область определения коэффициента детерминации – отрезок от нуля до единицы .

Коэффициент детерминации показывает, какая доля изменения зависимой переменной обусловлена изменениями объясняющей переменной.

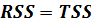Если , т.е. , означает, что регрессор x полностью обеспечивает весь размах изменения переменной y. В этом случае говорят, что спецификация модели, абсолютно качественная. Случайное возмущение во всех наблюдениях равно нулю.

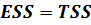Наоборот, если т.е. , означает, что весь размах изменения переменной y есть следствие воздействия неучтенных случайных факторов. В этом случае говорят, что спецификация модели абсолютно некачественная. Регрессор не оказывает влияния на формирование эндогенной переменной.

Замечание. Коэффициент детерминации 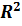имеет смысл только при наличии свободного коэффициента 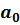в спецификации.

В случае парной линейной регрессии коэффициент детерминации равен квадрату коэффициента корреляции между переменными y и x.

Коэффициент детерминации величина случайная, т.к. его значение вычислено по случайной выборке. Следовательно, для тестирования гипотезы о том, что выбранный регрессор не оказывает влияние на формирование значения эндогенной переменной, согласно алгоритму проверки статистических гипотез, необходимо создать случайную переменную, связанную с гипотезой, закон распределения которой был бы известен. Если известна величина коэффициента детерминации, то в качестве такой переменной принимается переменная F_тест:

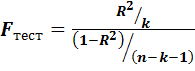(3.11)

Здесь: n – объем выборки;

k – количество регрессоров в модели (в нашем случае k=1);

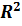- коэффициент детерминации.

Переменная F_тест подчиняется закону распределения Фишера с параметрами k и (n-k-1). Приняв значение доверительной вероятности, например, 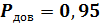, вычисляется критическое значение для переменной F_тест.

Если имеет место неравенство:

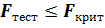(3.12)

То гипотеза о том, что регрессор x не влияет на формирование значения эндогенной переменной y, принимается. Если условие (3.12) не выполняется, то принимается альтернативная гипотеза о том, что регрессор x существенно влияет на формирование величины y. Можно показать, что гипотеза об отсутствии влияния регрессора на эндогенную переменную, эквивалентна гипотезе о равенстве нулю коэффициента детерминации.

Пример. Рассмотрим модель зависимости сбережений граждан от размера располагаемого дохода в Великобритании.

Таб. 3.3. Исходные данные и результат работы функции «ЛИНЕЙН»

Исходные данные для построения модели (выборка наблюдений), а также результат работы функции «ЛИНЕЙН» приведены в таб. 3.3.

Оцененная модель имеет вид:

Значение коэффициента детерминации равно:

Значение

Значение

Значение много больше , следовательно, оцененная модель имеет качественную спецификацию или, другими словами, выбранный регрессор влияет на формирование значения эндогенной переменной.

Дата добавления: 2015-10-29