Четвертый принцип спецификации модели

Рассмотрим конкретный пример. Предположим, изучается зависимость расходов на потребление от размера располагаемого дохода. В таб. 1.1 приведены данные, полученные в результате наблюдения за расходами в различных домашних хозяйствах.

Номер наблю-дения	Доход в долл. X	Расходы на потребление Y	Номер наблю-дения	Доход в долл. X	Расходы на потребление Y

Таб. 1.1. Таблица результатов наблюдений за расходами.

На рис.1.1 представлено графическое представление наблюдений. Это набор отдельных точек. Такой график называется диаграммой рассеяния.

Рис. 1.1. Диаграмма рассеяния.

Из диаграммы видно, что при одинаковом доходе расходы на потребление у различных потребителей отличаются.

Это означает, что функция описывающая зависимость расходов на потребление должна быть неоднозначной. С помощью линейной алгебраической функции такого результата добиться не возможно. Это утверждение справедливо и для любой другой модели. Естественно, хотелось бы иметь однозначное соответствие между значениями экзогенными (предопределенными) переменными и эндогенными переменными.

Что является причинами появления неоднозначности? Их две:

- индивидуальные особенности объекта;

- влияние других факторов, неучтенных в спецификации модели.

Например, если моделируются расходы на потребление мяса в зависимости от располагаемого дохода, то в качестве индивидуальной особенности может выступать отношение потребителя к мясу. Одни любят мясо, другие отдают предпочтение птице или рыбе, третьи его вообще не едят (вегетарианцы). Понятно, что при одинаковом располагаемом доходе эти потребители несут различные расходы на потребление мяса. С другой стороны, если вы собираете гостей, то, по такому случаю, вы купите больше мяса, чем обычно. Сбор гостей - пример фактора, повлиявшего на результаты наблюдения за расходами на мясо.

Для обеспечения однозначной зависимости между эндогенной и экзогенными переменными в уравнение модели вводится еще одна переменная, которую называют «случайное возмущение» или «остаток».

В результате, спецификацию модели в общем виде записывается как:

(1.6)

Определение. Модели, которые в своем составе содержат случайные возмущения, называются эконометрическими.

Рассмотренные ранее спецификации относят к экономическим моделям, т.е. моделям, которые обеспечивают однозначное соответствие между эндогенными и экзогенными переменными. В спецификации (1.6) функция описывает изменение эндогенной переменной в ответ на изменение экзогенных (предопределенных) переменных. Поэтому ее называют поведенческой частью модели или поведенческой функцией. Вид поведенческой функции в общем случае может быть любым.

В математике уравнения типа (1.6) называют обобщенной функциональной зависимостью или обобщенной регрессионной зависимостью.

Функцию в математике называют уравнением регрессии.

Переменная u_t является случайной величиной.

Ее назначение впитать в себя влияние всех особенностей экономического объекта и обеспечить однозначное соответствие между экзогенными и эндогенной переменной.

Остаток как случайная переменная определяется законом распределения (функцией плотности вероятностей). Будем предполагать, что случайное возмущение имеет математическое ожидание (среднее значение) равное нулю M(u_t)=0, а его дисперсия постоянна .

Если в правой части спецификации модели появилось случайное слагаемое, то и результат (эндогенная переменная) тоже становится случайной переменной со своей функцией плотности вероятностей.

Найдем математическое ожидание правой части модели (1.6).

(1.7)

Из выражения (1.7) следует, что функция описывает поведение среднего значения эндогенной переменной, а случайное возмущение определяет отклонение реального значения эндогенной переменной от своего среднего значения. Поэтому называют центрированным остатком.

Четвертый принцип спецификации модели заключается в необходимости учета случайных возмущений при записи уравнений модели.

С учетом сказанного спецификация эконометрической модели конкурентного рынка следует записать в виде:

(1.8)

Отметим. В модели (1.8) первые два уравнения называются поведенческими, а последнее тождеством.

Важно. Тождества не содержат случайных возмущений. Точнее говоря в тождествах случайные возмущения равны нулю.

Общий вид эконометрической модели. В общем случае эконометрическая модель имеет вид:

(1.9)

В спецификации (1.9):

- набор текущих эндогенных переменных;

- – набор предопределенных переменных;

- i=1,2,…m; j=1,2,…m – параметры при текущих эндогенных переменных;

- i=1,2,…,m; j=1,2,…k – параметры при предопределенных переменных.

Заметим, что среди предопределенных переменных мо;tn быть переменная тождественно равная единице (переменная при свободных параметрах).

Спецификация (1.9) называется точечного или координатного вида.

Спецификацию (1.9) можно записать в компактном виде. Для этого введем следующие обозначения:

- вектор текущих эндогенных переменных

– вектор предопределенных переменных

- вектор случайных возмущений (остатков)

матрица коэффициентов при текущих эндогенных переменных  

-

матрица коэффициентов при предопределенных переменных  

–

Тогда спецификацию модели (1.9) можно записать в виде:

(1.10)

Спецификация моделей может быть представлена в двух формах: структурной или приведенной.

Определение. Форма модели называется структурной, если хотя бы одно из ее уравнений содержит более одной текущей эндогенной переменной.

Определение. Форма модели называется приведенной, если в ее уравнениях каждая текущая эндогенная переменная выражена через предопределенные.

Спецификация (1.10) – компактная запись структурной формы эконометрической модели.

Решив систему уравнений (1.9) относительно текущих эндогенных переменных или, что все равно, систему (1.10) относительно вектора , получим приведенную форму той же модели. Общий вид приведенной формы модели имеет вид:

(1.11)

Замечание. (1.10) и (1.11) это одна и та же модель экономического объекта, записанная в различном виде.

От структурную форму модели всегда можно однозначно преобразовать в приведенную. Обратное не верно: не всегда от приведенной формы модели можно перейти к структурной.

Структурная форма модели, как правило, появляется на этапе спецификации, в уравнениях отражаются закономерности взаимодействия переменных. В структурной форме чаще всего удобно анализировать поведение экономического объекта.

В приведенной форме удобно решать задачу оценки значений параметров модели.

Из выражения (1.10) легко получить правило преобразования структурной формы модели в приведенную:

(1.12)

Пример. Преобразовать структурную форму спецификации модели конкурентного рынка (1.8) в приведенную форму.

(1.8)

Запишем необходимые вектора и матрицы:

При формировании векторов и матриц необходимо придерживаться следующих правил:

- Компоненты вектора могут быть представлены в любой последовательности, но после того, как вектор сформирован, изменение последовательности не допускается.

- В векторе на первое место принято ставить «1» (псевдопеременная при свободных параметрах), если хотя бы в одном из уравнений модели присутствует свободный коэффициент.

- Чтобы сформировать первую строку матрицы A, достаточно взять первое уравнение модели и записать коэффициенты, стоящие перед каждой компонентой вектора, в той последовательности, в какой они зафиксированы. Аналогичным образом формируются остальные строки матрицы. При этом необходимо помнить, что в каноническом виде в уравнениях модели справа стоят только случайные возмущения.

- Матрица B формируется по тому же правило, только относительно вектора Х.

- Вектор U формируется из остатков. При этом необходимо помнить, что в тождествах случайное возмущение формально присутствует и равно нулю.

Замечание. Матрица А всегда квадратная (второй принцип спецификации), матрица В может быть любой.

Теперь для преобразования структурной формы модели в приведенную необходимо вычислить компоненты матрицы М и вектора по правилам (1.12).

Обратная матрица может быть вычислена либо методом Гаусса, либо через матрицу алгебраических дополнений.

Опуская вычисление обратной матрицы, запишем результат:

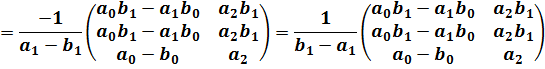
В результате приведенная форма модели конкурентного рынка принимает вид:

(1.13)

Для того, чтобы получить точечную запись приведенной формы модели, достаточно произвести необходимые алгебраические действия.

(1.14)

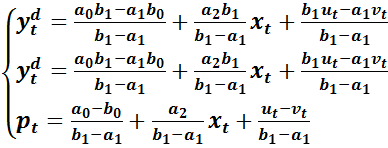
Система уравнений (1.14) – точечная запись приведенной формы модели конкурентного рынка.

---

Дата добавления: 2015-10-29