Подведем итог. 1. Вы познакомились с целями и задачей эконометрики как науки.

1. Вы познакомились с целями и задачей эконометрики как науки.

2. Дали классификацию переменных модели (объекта): «эндогенные переменные», «экзогенные переменные», «датированные переменные», «лаговые переменные», «предопределенные переменные».

3. Дали классификацию моделей: «открытая модель», «замкнутая модель».

4. Уяснили, что в отличие от экономической модели, эконометрическая модель содержит в своем составе случайную составляющую (случайное возмущение).

5. Поняли, что модель может быть представлена в двух формах: «структурной» и «приведенной».

6. Получили универсальные формулы вычисления параметров приведенной формы модели по известным параметрам ее структурной формы.

Задачи для самоконтроля

1. Определение эконометрики как науки.

2. Определение модели экономического объекта.

3. Элементы математической модели.

4. Рассмотрением, какого вида моделей ограничивается эконометрика.

5. Этапы построения математических моделей.

6. Содержание этапа спецификации модели.

7. Принципы спецификации модели.

8. Понятия эндогенной, экзогенной и предопределенной переменных.

9. Общий вид экономической модели в координатном и векторном виде.

10. Чем отличается эконометрическая модель от экономической.

11. Чем вызвана необходимость введения в экономическую модель случайного возмущения.

12. Формы представления эконометрических моделей.

13. Правила преобразования структурной формы модели к приведенной.

Лекция 2. Оценивание параметров линейной модели

Множественной регрессии

Содержание лекции

1. Понятие оценки и требования, которые к ним предъявляются.

2. Метод наименьших квадратов как инструмент оценивания параметров модели.

3. Теорема Гаусса-Маркова, ее содержание и назначение.

4. Оценка параметров модели парной линейной регрессии.

5. Вычисление оценок параметров линейных регрессионных моделей с помощью ПЭВМ.

Мы обсудили первый этап построения модели, а именно, спецификацию модели.

Второй этап построения модели – это сбор исходной информации. Имея запись спецификации модели, понятно, за какими переменными модели необходимо пронаблюдать и зафиксировать значения.

Отметим, что это очень ответственный этап, который во многом определяет успех построения модели. В результате выполнения этого этапа в распоряжении исследователя появляются необходимые для построения модели данные, которые принято называть выборкой.

Мы не останавливаемся подробно на особенностях второго этапа, предполагая, что с ним Вы познакомились в процессе освоения дисциплины теории вероятностей и математической статистики.

Переходим к обсуждению третьего этапа построения модели: этапу оценивания (идентификации) модели. Его называют математическим, вычислительным или идентификационным.

В результате первой лекции мы установили, что эконометрическая модель оперирует со случайными переменными. Наличие случайного слагаемого в правой части модели приводит к тому, что и левая часть приобретает случайный характер.

Вспомним, что любая случайная величина характеризуется присущим ей законом распределения (функцией плотности вероятности для непрерывных случайных величин). Законы распределения случайных величин содержат параметры. Наша задача научиться оценивать их значения.

Начнем с понятия «оценка». По определению оценка – это приближенное значение параметра.

Далее будем рассматривать только эконометрические модели в виде изолированного уравнения:

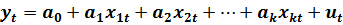(2.1)

Спецификация модели (2.1) содержит k экзогенных переменных (регрессоров).

Из (2.1) следует, что значение случайного наблюдения можно оценить как:

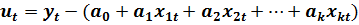(2.2)

Пусть известна функция распределения вероятностей случайной переменной u_t, тогда эту функцию можно записать с учетом выражения (2.2). Например, пусть случайное возмущение подчиняется нормальному закону распределения с параметрами (0, σ_u). Тогда функция распределения примет вид:

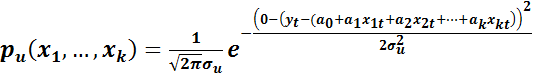(2.3)

В результате параметры модели (2.1) оказались параметрами функции плотности вероятностей.

Задача оценки параметров модели, превратилась в задачу оценки параметров закона распределения.

Вспомним. Параметры любого закона распределения и его количественные характеристики – это константы, но оценка этих параметров и количественных характеристик суть величины случайные.

Что бы отличать параметры от их оценок, будем их обозначать в виде имени параметра с волнистой чертой.

Остановимся на требованиях, которые будем предъявлять к оценкам. Таких требований два: несмещенность и эффективность.

Определение. Оценка параметра закона распределения называется несмещенной, если ее математическое ожидание совпадает со значением параметра: .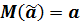

На практике можно предложить множество процедур расчета несмещенных оценок параметров.

Пример. Пусть рассматривается некоторая случайная величина x c известным законом распределения. Необходимо подобрать процедуру оценки среднего значения (математического ожидания) этой величины.

Для вычисления оценки имеем выборку из двух наблюдений x₁ и x₂.

Для элементов выборки должны выполняться условия:

- все элементы выборки независимые случайные величины;

- все элементы выборки имеют одинаковый закон распределения, совпадающий с законом распределения самой случайной величины.

Известно, что оценку среднего значения проводят по формуле:

(2.4)

Найдем альтернативные процедуры, которые позволяют так же получить несмещенные оценки среднего значения. Пусть такая процедура выглядит так:

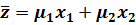(2.5)

Математическое ожидание такой оценки с учетом статистических свойств выборки есть:

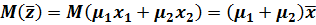(2.6)

Отсюда видно, что математические ожидания случайной величины x, полученные по формулам (2.4) и (2.6) будут совпадать при условии:

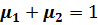(2.7)

Мы получили бесконечное количество процедур, которые обеспечивают несмещенные оценки среднего значения.

Для того, чтобы выбрать наилучшую процедуру оценки используют критерий минимальности дисперсии оценки.

Определение. Эффективной среди всех несмещенных оценок параметра называется та оценка, которая имеет минимальную дисперсию.

Другими словами, выбирается та процедура вычисления оценки, которая дает минимальный разброс значений оценки.

Найдем, при каких значениях 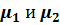дисперсия выражения (2.5) будет минимальной. Дисперсия 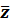с учетом независимости x₁ и x₂ имеет вид

Для нахождения минимума функции W необходимо приравнять ее производную по μ₁ нулю и из полученного уравнения найти значение μ₁. С учетом, что по свойству выборки дисперсии наблюдений равны, получим:

Откуда получаем, что процедура (2.5) дает наилучшую (нес-мещенную и эффективную) оценку среднего значения при .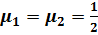

Далеко не всегда удается подобрать процедуру, которая обеспечивала получение несмещенных и эффективных оценок при конечном (небольшом) объеме выборки.

Вводятся понятия асимптотически несмещенных и асимптотически эффективных оценок, оценок для которых свойства несмещенности и эффективности достигаются при неограниченном увеличении объема выборки.

Однако и такие оценки получаются не всегда. Нас будут удовлетворять оценки, обладающие только свойством несмещенности при больших выборках. Такие оценки называют состоятельными.

Одним из методов, позволяющих получение, по крайней мере, состоятельных оценок, является метод наименьших квадратов (МНК).

Метод наименьших квадратов. Этот метод был предложен Гауссом еще в 18 веке. Гаусс решал задачу о том, как на плоскости (в пространстве) через известный набор точек провести прямую наилучшим способом. В качестве критерия он предложил использовать сумму квадратов остатков (невязок), т.е. разностей между абсциссами реальных точек и соответствующих им точек, лежащих на прямой. В математике решение такой задачи получило название регрессионного анализа.

Рассмотрим механизм применения МНК на примере идентификации модели в виде линейного уравнения парной регрессии:

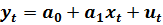(2.8)

Для решения задачи имеем набор точек на плоскости или другими словами набор наблюдений за поведением переменных y и x размером n наблюдений.

Таблица исходных данных (выборка)

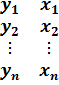
Согласно методу наименьших квадратов, необходимо найти такие значения оценок параметров модели (2.8), которые соответствуют минимуму суммы квадратов остатков.

Из (2.8) следует, что необходимо найти минимум функции:

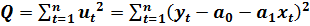(2.9)

Для нахождения параметров функции (2.9), соответствующие ее минимуму, необходимо вычислить производные этой функции по параметрам, приравнять их нулю и решить полученные уравнения относительно 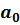и .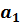

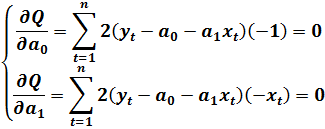
Разделив обе части уравнений на «-2» и выполнив перемножения, получим:

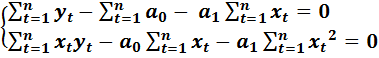(2.10)

Или окончательно получаем:

(2.11)

Система уравнений (2.11) называется системой нормальных уравнений для определения оценок параметров модели (2.8).

Убедимся, что решения системы уравнений (2.11) соответствуют минимуму функции (2.9). Для этого достаточно показать, что вторые производные функции (2.9) положительны.

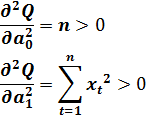
Систему уравнений (2.11) можно решить методом исключения переменных. Для этого достаточно выразить параметр 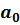через 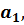подставить его во второе уравнение системы, откуда легко получить 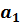, затем полученное значение 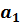подставить в первое уравнение и получить выражение для 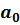. В результате решение системы уравнений (2.11) примет вид:

(2.12)

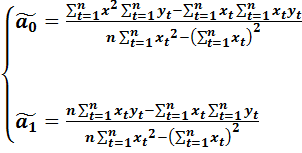
Выражения (2.12) позволяют по известным значениям наблюдений за переменными x и y вычислить оценки параметров модели парной регрессии.

Проверим, насколько полученные оценки отвечают требованию несмещенности. Для этого запишем второе выражение (2.12) в виде:

(2.13)

Для получения выражения (2.13) необходимо вспомнить, что оценка ковариации и дисперсии случайных переменных вычисляются, как:

(2.14)

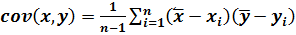
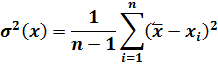
Раскрыв скобки и произведя несложные преобразования, легко получить выражение (2.13).

Преобразуем (2.13) к виду:

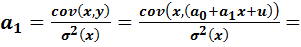
(2.15)

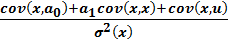
Первое слагаемое в выражении (2.15) равно нулю, т.к. параметр 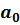константа, а cov(x,x)=σ²(x). Тогда окончательно выражение (2.15) принимает вид:

(2.16)

Математическое ожидание оценки параметра 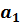равно правой части выражения (2.16), т.к. параметр и количественные характеристики случайных переменных константы.

Отсюда видно, не смотря на то, что случайные возмущения напрямую не учувствуют в вычислении значений оценок параметров, они существенно влияют на их качество, а именно, если случайное возмущение коррелирует с регрессором, то значение оценки становится смещенным.

Вывод. Применение МНК к оценке параметров линейной алгебраической модели не всегда позволяет получить состоятельные оценки. Для получения состоятельных оценок необходимо, чтобы случайные возмущения удовлетворяли ряду условий. Эти условия сформулированы в теореме Гаусса-Маркова.

---

Дата добавления: 2015-10-29