Возмущений, взвешенный метод наименьших квадратов

Продолжая анализ построенной модели, рассмотрим следующие вопросы:

1. Понятие гетероскедастичности.

2. Последствия гетероскедастичности

3. Тест Голдфельда-Квандта

4. Тест ранговой корреляции Спирмена

5. Исправление гетероскедастичности, взвешенный метод наименьших квадратов

Мы уже познакомились с тремя стадиями подготовки эконометрических моделей в виде уравнений множественной линейной регрессии. Мы знаем, как записать спецификацию модели, знаем, что под эту спецификацию необходимо собрать опытные данные (выборка результатов наблюдений), разобрались в формулировке теоремы Гаусса-Маркова и научились отыскивать оценки параметров модели и их стандартные ошибки, приступили к анализу полученных результатов. Начали анализ с качества спецификации модели, а теперь, имея качественную спецификацию, приступаем к проверке гипотез о выполнении предпосылок теоремы Гаусса-Маркова, чтобы понять насколько полученные оценки удовлетворяют свойству состоятельности.

Первая предпосылка теоремы Гаусса-Маркова требует, чтобы математическое ожидание случайных возмущений во всех наблюдениях было нулевым: 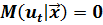. Мы уже отмечали, что невыполнение этого условия приводит к смещению оценок параметров модели.

Важное для практики условие. Но оно, как правило, не проверяется, т.к. МНК автоматически обеспечивает выполнение первой предпосылки теоремы Гаусса-Маркова, если в спецификации модели содержится свободный коэффициент .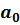

Поэтому сразу переходим к обсуждению второй предпосылки теоремы: условию гомоскедастичности, или однородности, или одинаковости дисперсий случайных возмущений во всех наблюдениях (.

Начнем с понятии гомоскедастчности. Разберемся, почему мы говорим о количественных характеристиках переменной u_t в наблюдениях. Ведь мы имеем лишь одно i – ое наблюдение. Предполагается следующая ситуация. Рассмотрим для определенности первое наблюдение i=1. Получив первую выборку результатов наблюдений за переменными модели, увидим, что в первом наблюдении случайное возмущение получило значение u₁. Если получить вторую выборку наблюдений за тем же объектом того же объема, то окажется, что во второй выборке в первом наблюдении случайное возмущение имеет значение u₂. Сделав, m выборок, получим набор значений случайной переменной u, оказавшихся на месте первого наблюдения. Другими словами, переменная u_t в каждом наблюдении выборки, представляет собой условное распределение случайной переменной. Условное, потому что это распределение соответствует заданному значению вектора экзогенных переменных .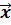

Это относится и к значению эндогенной переменной. Эндогенная переменная y при каждом фиксированном значении вектора 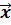представляет собой условное распределение случайной величины.

Гомоскедастичность – это ситуация, в которой случайные возмущения подчиняются одному и тому же закону распределения. Пример гомоскедастичной модели приведен на рис. 4.1.

Предполагается, что в этой модели случайное возмущение подчиняется нормальному закону распределения N(0; σ_u) с одинаковыми параметрами.

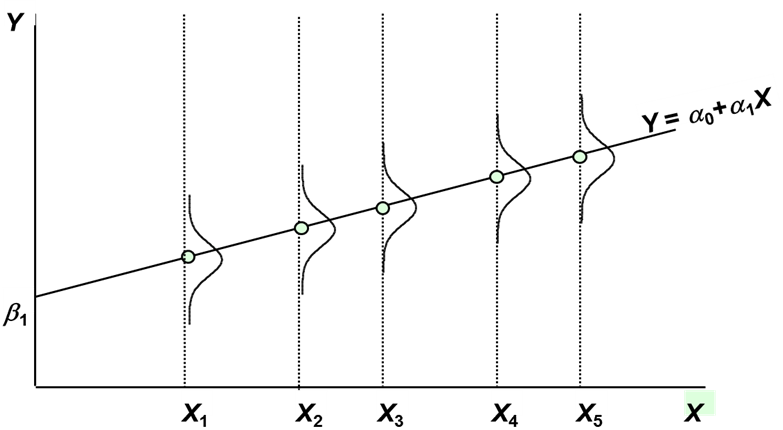
Рис. 4.1. Пример эконометрической модели с гомоскедастичными

остатками.

На рис. 4.2. приведен пример модели с гетероскедастичными остатками. Предполагается, что вид закона распределения в каждом условном распределении одинаковый, но значение параметра σ в них отличаются.

Рис. 4.2. Пример модели с гетероскедастичными остатками.

Последствиями гетероскедастичности случайных возмущений является потеря несмещенности значений стандартных ошибок параметров. Ошибки значений параметров оказываются завышенными. Это, в свою очередь, может привести к некорректности результатов тестирования статистической значимости параметров линейной модели. Действительно, в основе теста лежит дробь Стьюдента:

.

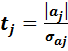Если ошибка 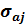завышена, то значение дроби Стьюдента оказывается заниженным и возможна ситуация, что причиной принятия гипотезы 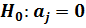является завышенное значение ошибки параметра, а не его статистическая незначимость.

Тестирование модели на отсутствие гетероскедастичности. В основу идей тестов моделей на присутствие гетероскедастичности лежит предположение о том, что гетероскедастичность есть результат зависимости дисперсий случайных возмущений от абсолютных значений регрессоров. Это предположение сделано на основе опытных данных: замечено, что ошибка случайных возмущений чаще всего растет с ростом абсолютных значений регрессоров. Например, рассмотрим модель зависимости государственных расходов на образование от объема ВВП. Рассмотрим два государства: США и Куба. ВВП США исчисляется в триллионах долларов, ВВП Кубы в десятках миллиардов долларов. Практика показывает, что на образование государства расходуют 3% - 5% ВВП. Эти 3% - 5% ВВП в США на несколько порядков превосходят 3% - 5% для Кубы. Естественно, что и разброс значений расходов на образование во времени в США значительно выше, чем на Кубе.

Для тестирования гетероскедастичности используются несколько тестов. Мы познакомимся с двумя из них.

Наиболее популярным является тест Голдфельда-Квандта. Он построен на двух предположениях:

- ошибки случайных возмущений зависят от абсолютных значений регрессоров;

- случайные возмущения имеют нормальный закон распределения.

Идея теста проста. Раз мы предположили, что ошибка случайного возмущения зависит от абсолютных значений регрессоров, давайте поступим следующим образом. Сформируем из имеющейся выборки наблюдений две группы, в которых объединим наблюдения с небольшими значениями регрессоров и с большими значениями регрессоров. Построим модели по этим группам наблюдений и проверим гипотезу о том, что ошибки случайных возмущений для этих моделей будут одинаковыми. Если это так, то можно считать, что модель в целом гомоскедастична.

Приступим к реализации идеи. Рассмотрим процесс тестирования гетероскедастичности с помощью теста Голдфельда-Квандта в виде алгоритма.

Шаг 1. В качестве показателя веса абсолютных значений регрессоров в наблюдении примем величину:

(4.1)

Замечание. Переменная не является регрессором модели, а служит только для решения поставленной задачи.

Замечание. Константа «1» в (4.1) – регрессор, стоящий при параметре 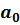, если свободный параметр отсутствует в спецификации линейной модели множественной регрессии, то и константа «1» отсутствует в выражении (4.1).

В (4.1) суммируются абсолютные значения регрессоров в одном наблюдении.

Будем предполагать, что ошибка случайного возмущения пропорциональна весу регрессоров (4.1):

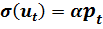(4.2)

Шаг 2. Имеющаяся выборка наблюдений за переменными экономического объекта сортируется по возрастанию (убыванию) значений переменной .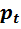

В результате выполнения этого шага строки в выборке наблюдений расположатся так, что в ее начале соберутся наблюдения с небольшими весами регрессоров, а в ее конце – наблюдения с большими значениями веса регрессоров.

Шаг3. Отсортированная таким образом выборка делится на три примерно равные по объему части.

В результате этого действия получим два фрагмента выборки. В первой трети выборки будут собраны наблюдения с небольшим весом регрессоров, в последней – наблюдения с большим весом регрессоров.

Замечание. Средний фрагмент выборки исключается из рассмотрения при дальнейшей реализации теста Голдфельда-Квандта.

Шаг 4. Для первого и третьего фрагментов выборки независимо оцениваются модели линейной регрессии:

В результате оценки для каждой модели можно получить значение дисперсии случайного возмущения и .

Статистическая гипотеза, которая подвергается тестированию, имеет вид:

Для проверки гипотезы вводится случайные переменные (статистики):

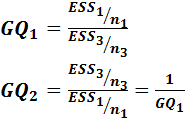(4.3)

Обе переменные подчиняются закону распределения Фишера с параметрам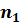и и 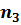. Следовательно, для заданного значения доверительной вероятности P_дов (уровня значимости критерия α) можно найти критическое значение дроби Фишера F_крит, сравнив с которым вычисленные значения статистик 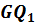и , можно сделать вывод о принятии выдвинутой гипотезы.

Гипотеза о равенстве дисперсий во фрагментах выборки принимается, если:

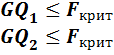(4.4)

Замечание. Для удобства вычислений на практике разбиение исходной выборки на фрагменты осуществляется таким образом, чтобы объемы первого и третьего фрагментов были равны: 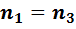. Тогда значения статистик Голдфелда-Квандта (4.3) примут более простой вид:

(4.5)

Пример. Построить и протестировать на отсутствие гетероскедастичности модель «государственные расходы на образование в зависимости от объема ВВП.

В таб. 4.1 приведены данные по государственным расходам на образование и ВВП в различных странах.

Данные отсортированы по возрастанию величины 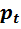, жирным шрифтом выделены первый и третий фрагменты выборки.

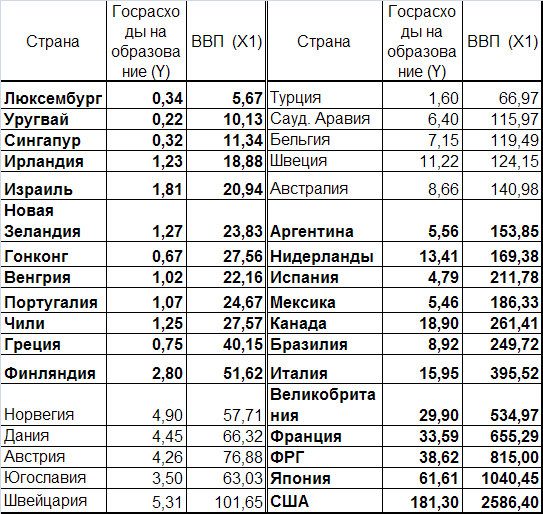
Таб. 4.1. Государственные расходы на образование.

Результаты оценки моделей по фрагментам выборки приведены на рис. 4.3.

Жирным шрифтом выделены значения ESS.

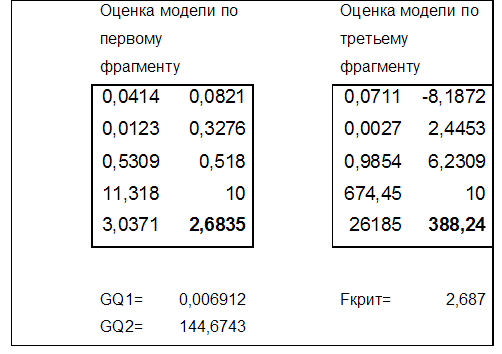
Рис. 4.3. Результаты тестирования модели на гомоскедастичность.

Из приведенных данных, очевидно, что гипотеза о гомоскедастичности случайных возмущений отклоняется.

Тест ранговой корреляции Спирмена. В основу теста также положено предположение о том, что дисперсия случайного возмущения связана с абсолютными значениями регрессоров.

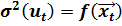
При этом никаких дополнительных предположений относительно вида функции 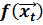или ограничений на закон распределения случайных возмущений не делается. Идея теста заключается в том, что величина остатков является оценкой ее стандартной ошибки. Поэтому в случае гетероскедастичности абсолютные значения остатков и абсолютные значения вектора регрессоров будут коррелированными.

Тест Спирмена основан на вычислении коэффициента ранговой корреляции между случайными возмущениями и абсолютными значениями вектора .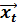

(4.6)

где: n – объем выборки;

D_t – разность между рангами по абсолютным значениям вектора 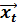и случайного возмущения .

Замечание. Под рангом понимается порядковый номер наблюдения в выборке, отсортированной по значению модуля (ранг по ) или по 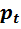(ранг по вектору ).

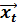В случае отсутствия гетероскедастичности, значение коэффициента ранговой корреляции 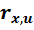должен равняться нулю, т.е. основная гипотеза принимает вид . Т.к. закон распределения случайной переменной 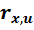не известен, то для тестирования гипотезы формируется случайная переменная:

(4.7)

Случайная переменная 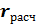подчиняется нормальному закону распределения N(0; 1/(n-1)), при условии, что 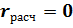. Для нормального распределения можно вычислить для заданной доверительной вероятности критическое значение и, если выполняется условие 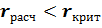, то нулевая гипотеза об отсутствии гетероскедастичности принимается.

Пример. Провести тестирование на гетероскедастичность случайных возмущений с помощью теста Спирмена для задачи моделирования объема государственных расходов в различных странах от ВВП. (Рассмотренный ранее пример). На рис. 4.4. Приведены исходные данные, рассчитанные значения модулей случайных возмущений и ранги по весу вектора 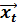и абсолютному значению .

Замечание. На практике ранжирование выборки наблюдений с помощью приложения EXCEL не сложно. Для этого достаточно вначале отсортировать строки выборки по Х (в общем случае по 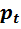) и пронумеровать их в полученном порядке. Вы получите значения рангов по Х. Затем отсортировать выборку по абсолютным значениям , вновь пронумеровать результат сортировки. Получится столбец, содержащий значения рангов по .

По полученным данным вычисляется столбец .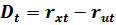

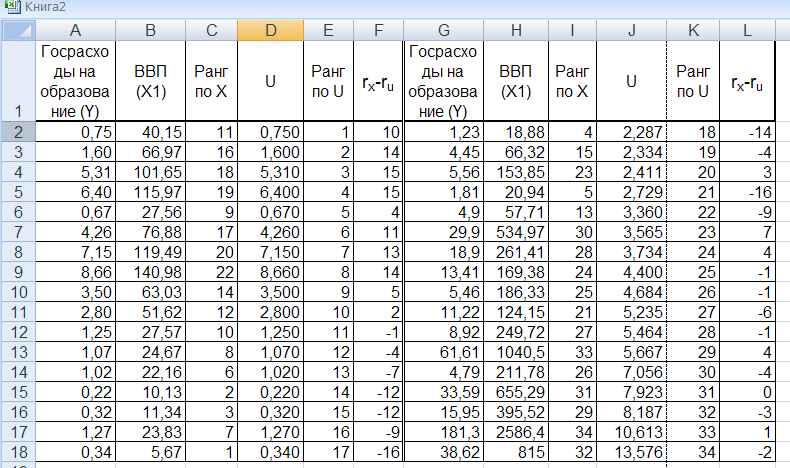
Рис. 4.4. Результаты расчетов для применения теста Спирмена.

В результате получаем:

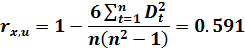
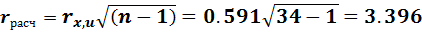
Полученное значение 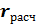необходимо сравнить с двусторонней квантилью нормального распределения при Р_дов=0.95 (α=0.05) и параметрами (0;1/33). Это значение можно вычислить с помощью функции 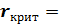НОРМОБР(0.05; 0.3)=2.58.

Т.к. условие 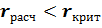не выполняется, гипотеза об отсутствии гетероскедастичности отклоняется.

Как видно, оба теста привели к одинаковому результату.

Вопрос, на который предстоит ответить – что же делать, если случайные возмущения оказались гетероскедастичными.

Оценка параметров линейной модели в условиях гетероскедастичности.

Подход к решению проблемы устранения гетероскедастичности сводится к искусственному преобразованию спецификации модели таким образом, чтобы условие гомоскедастичности выполнялось тождественно. Для понимания этого подхода начнем рассмотрение вопроса с частного случая, а именно случая, когда известны дисперсии случайных возмущений в каждом наблюдении.

И так, имеем спецификацию модели множественной линейной регрессии, выборку наблюдений за переменными модели для ее идентификации и множество значений дисперсии соответствующих каждому наблюдению. Разделим левую и правую части модели на соответствующее значение стандартной ошибки (корень из дисперсии):

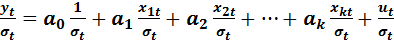(4.7)

Найдем количественные характеристики величины :

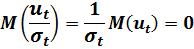
Получилось, что во всех наблюдениях величина 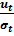имеет нулевое математическое ожидание и постоянную дисперсию. Если ввести новые переменные

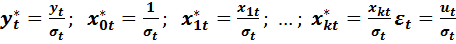(4.8)

и сделать замену переменных, то получим спецификацию модели в виде:

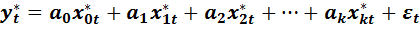(4.9)

Спецификация (4.9) вновь представляет собой линейную модель множественной регрессии. Для нее необходимо создать выборку наблюдений за переменными (4.8), по ним оценить модель (4.9), убедиться в ее качестве и вновь проверить на гомоскедастичность.

Замечание. Обратите внимание на то, что в спецификации (4.9) отсутствует свободный от регрессора параметр. При параметре 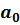появился регрессор .

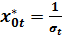Неудобство такого подхода заключается в том, что им на практике невозможно воспользоваться. Как правило, нет возможности априори оценить ошибку случайных возмущений в каждом уравнении.

Вместе с тем, этот пример подсказывает направление действий для устранения гетероскедастичности. Необходимо задать правило вычисления стандартных ошибок случайных возмущений, разделить на эти ошибки переменные модели и сделать замену переменных. В результате появляется возможность получить модель с гомоскедастичными остатками.

Воспользуемся предположением тестов Глдфелда-Квандта и Спирмена о том, что ошибки случайных возмущений связаны с абсолютными значениями регрессоров. Предположим, что стандартную ошибку случайных возмущений, можно представить в виде:

(4.10)

где: 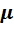- показатель степени, с помощью которого учитывается возможность нелинейной связи между ошибкой остатка и абсолютным весом регрессоров.

Разделив модель (4.7) на (4.10), получим:

(4.11)

Количественные характеристики случайной переменной :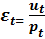

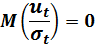
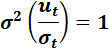
Введя новые переменные

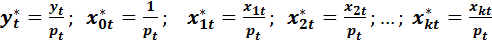(4.12)

и сделав соответствующую замену, вновь получим модель в виде линейного алгебраического уравнения с гомоскедастичными остатками.

Остается открытым вопрос о значении 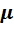. Начинают процесс устранения гетероскедастичности со значения . Если при модель (4.11) остается гетероскедастичной, то вводится приращение 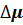(например 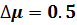) и модель (4.11) проверяется на гетероскедастичность при 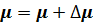. Меняя знак и абсолютное значение приращения 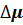, добиваются выполнения соотношений (4.5).

Функцию (4.10) называют весовой функцией. Заметим, что в спецификации модели вида (4.11) значения 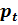во всех наблюдениях будут равны. Говорят, что преобразование (4.12) выравнивает веса регрессоров во всех наблюдениях.

Пример. При построении модели государственных расходов на образование от объема ВВП выяснилось (см. рис. 4.4), что модель имеет гетероскедастичные остатки, т.е. гипотеза о выполнении второй предпосылки теоремы Гаусса-Маркова не принимается.

Применим описанный выше алгоритм для исправления гетероскедастичности. Примем , вычислим значения

для каждого наблюдения и разделим на него значения Y, x₁ и введем регрессор (таб. 4.4).

В таб. 4.4. Приведены результаты исправления гетероскедастичности: значения преобразованных переменных и проверка полученной модели на гомоскедастичность. Затенены фрагменты выборки и значения ESS. Как видно из приведенных данных, исправить гетероскедастичность удалось уже при .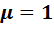

№	Страна	Y/P	x0=1/P	X1/P
	Люксембург	0,0510	0,1499	0,8501
	Уругвай	0,0198	0,0898	0,9102
	Сингапур	0,0259	0,0810	0,9190
	Ирландия	0,0619	0,0503	0,9497
	Израиль	0,0825	0,0456	0,9544
					Продолжение таблицы
	Новая Зел.	0,0511	0,0403	0,9597
	Гонконг	0,0235	0,0350	0,9650		0,0442	0,0237	0,0000
	Венгрия	0,0440	0,0432	0,9568		0,0106	0,1558	#Н/Д
	Португалия	0,0417	0,0390	0,9610		0,8484	0,0199	#Н/Д
	Чили	0,0438	0,0350	0,9650		27,9826	10,0000	#Н/Д
	Греция	0,0182	0,0243	0,9757		0,0222	0,0040	#Н/Д
	Финляндия	0,0532	0,0190	0,9810
	Норвегия	0,0835	0,0170	0,9830
	Дания	0,0661	0,0149	0,9851		GQ1=	1,24746
	Австрия	0,0547	0,0128	0,9872		GQ2=	0,80162
	Югославия	0,0547	0,0156	0,9844		Fкрит=	2,68663
	Швейцария	0,0517	0,0097	0,9903
	Турция	0,0235	0,0147	0,9853
	Сауд. Аравия	0,0547	0,0085	0,9915
	Бельгия	0,0593	0,0083	0,9917
	Швеция	0,0897	0,0080	0,9920
	Австралия	0,0610	0,0070	0,9930
	Аргентина	0,0359	0,0065	0,9935		0,0585	-2,6350	0,0000
	Нидерланды	0,0787	0,0059	0,9941		0,0098	2,5834	#Н/Д
	Испания	0,0225	0,0047	0,9953		0,9043	0,0178	#Н/Д
	Мексика	0,0291	0,0053	0,9947		47,2491	10,0000	#Н/Д
	Канада	0,0720	0,0038	0,9962		0,0301	0,0032	#Н/Д
	Бразилия	0,0356	0,0040	0,9960
	Италия	0,0402	0,0025	0,9975
	Великобр.	0,0558	0,0019	0,9981
	Франция	0,0512	0,0015	0,9985
	ФРГ	0,0473	0,0012	0,9988
	Япония	0,0592	0,0010	0,9990
	США	0,0701	0,0004	0,9996

Таб. 4.4. Результат преобразования модели к гомоскедастичному виду.

На рис. 4.5. Приведены диаграмма рассеяния исходных данных и графики двух моделей: серая линия – модель гетероскедастичная, черная линия - модель гомоскедастичная.

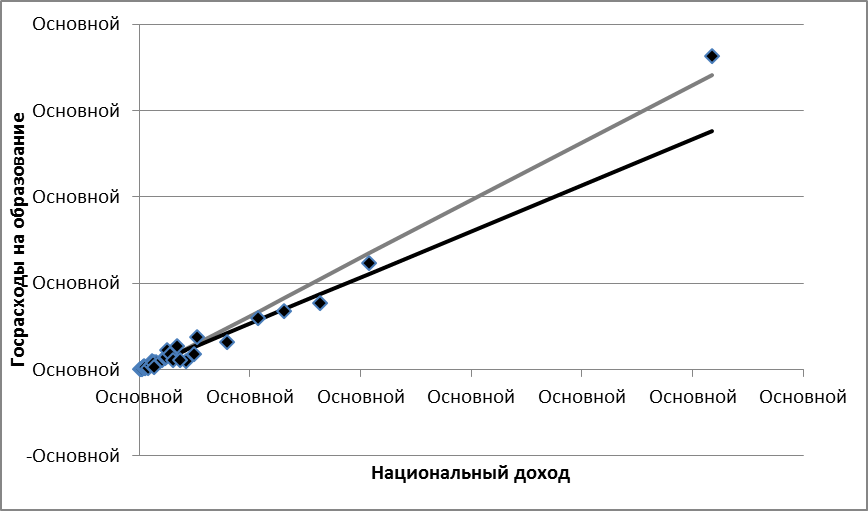
Рис. 4.5. Диаграмма рассеяния и графики гетероскедастичной и гомоскедастичной моделей.

Как видно на рис. 4.5. гомоскедастичная модель, в данном случае, проходит ниже гетероскедастичной. Это является следствием того, что при исправлении гетероскедастичности остатков регрессии больший вес был придан наблюдениям с небольшими значениями ВВП. Т.к. данные в выборке оказались неравномерно рассредоточены по области определения, то и их влияние на формирование эндогенной переменной тоже оказалось неодинаковым. Больший вес придан тем данным, количество которых было больше.

Еще один пример. Оценить и проанализировать на присутствие гетероскедастичности модель зависимости расходов на жилье в зависимости от располагаемого дохода и индекса цен на жилье.

На рис. 4.6. приведены выборка данных наблюдения, значения вспомогательной переменной 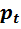при μ=1, результаты применения функции «ЛИНЕЙН» к первой и последней третям выборки (n₁=n₃=9), значения GQ₁ и GQ₂, а также значение Fкрит при α=0,05.

Рис.4.6. Результат анализа модели на гомоскедастичность

Спецификация модели имеет вид:

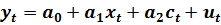
Ограничимся только тестированием модели на гомоскедастичность остатков, опустив анализ качества спецификации.

Приведенные данные отсортированы по переменной p_t. В таблице данные, по которым проводится анализ, затенены, а значения ESS₁ и ESS₃ выделены жирным шрифтом.

Приведенные результаты свидетельствуют о наличии гетероскедастичности.

Исправление гетероскедастичности начинаем при μ=1. На рис. 4.7. приведены данные для оценки спецификации вида:

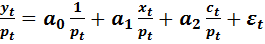(4.13)

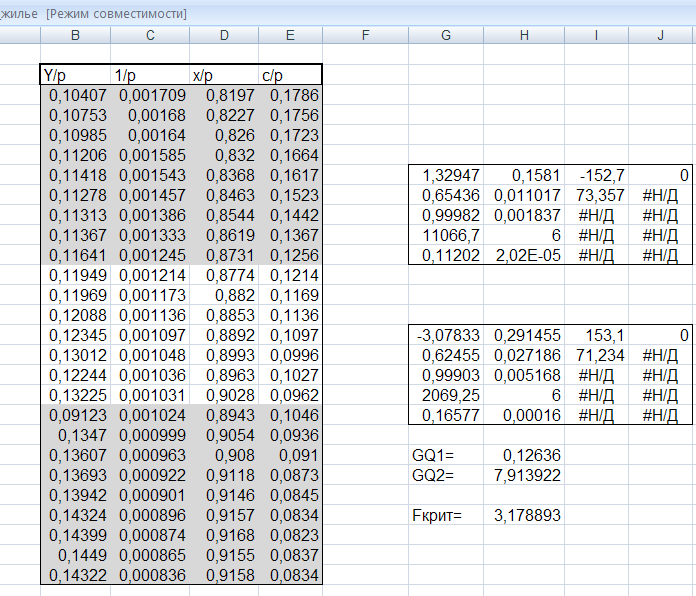
Рис. 4.7. Данные и результаты анализа модели (4.13).

Видно, что при μ=1 модель осталась гетероскедастичной, исправить модель не удалось.

В таб. 4.5. Приведены расчеты для ряда значений μ.

Расчеты проведены с шагом 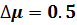. Видно, что при μ=2.0 модель становится гомоскедастичной, а при μ=2.5 условие гомоскедастичности выполняется еще более строго.

Таблица 4.5.

	GQ1	GQ2	Fкрит
μ=1.0	0.13	7.91	3.18
μ=1.5	0.20	4.80
μ=2.0	0.32	3.02
μ=2.5	0.53	1.88

При дальнейшей вариации абсолютным значением и знаком 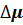методом половинного деления можно было добиться выполнения соотношения GQ₁=GQ₂=1. Но в этом необходимости нет, т.к. в условиях стохастичности достаточно выполнения такой гипотезы в статистическом смысле при заданной доверительной вероятности. Процесс подбора значения μ можно остановить на μ=2.0.

Взвешенный метод наименьших квадратов (ВМНК)

Давайте поймем, что собственно мы делали для устранения гетероскедастичности.

1. Подобрали функцию вида .

2. Каждое наблюдение в выборке умножили на .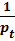

3. К преобразованной таким образом выборке применили метод наименьших квадратов для получения оценок параметров модели.

Как это выглядит математически. Введем матрицу W размерностью

(n x k):

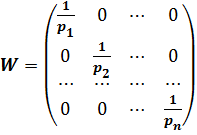(4.14)

Тогда преобразование переменных можно представить в виде произведени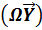й: и 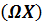, процедура метода наименьших квадратов примет вид:

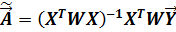(4.15)

Процедура (4.15) обеспечила получение состоятельных оценок параметров линейной модели при выполнении всех предпосылок теоремы Гаусса-Маркова, кроме второй, предпосылки о гомоскедастичности случайных возмущений.

Этот факт нашел свое отражение в теореме. Прежде, чем ее сформулировать, введем матрицу ковариаций вектора случайных возмущений в виде:

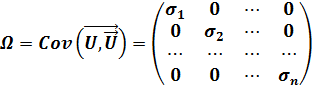(4.16)

Теорема. Если в схеме Гаусса-Маркова ковариационная матрица вектора случайных возмущений имеет вид (4.16), то оптимальной процедурой, доставляющей состоятельные оценки параметров линейной модели, является:

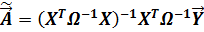(4.17)

Процедура (4.17) называется взвешенным методом наименьших квадратов.

Дата добавления: 2015-10-29