Шаг 3. Задается значение доверительной вероятности .

Область определения созданной случайной переменной z разбивается на две непересекающихся области: область, где выдвинутая гипотеза принимается 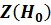, и область, где основная гипотеза отклоняется .

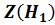Разбиение области определения созданной случайной переменной осуществляется таким образом, чтобы оказалось справедливым равенство:

Это означает, что вероятность попадания случайной переменной z в область 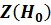при условии, что гипотеза истинна, равна принятой доверительной вероятности. Другими словами, в области определения переменной z выделяется участок, внутри которого случайное событие 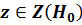оказалось практически достоверным событием при условии, что гипотеза истинна.

Граница, разделяющая область определения случайной переменной z, называется критическим значением распределения.

Шаг 4. Проверяется появление случайного события 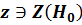. Если событие появилось, то гипотеза принимается как непротиворечащая опытным данным, если оно не появилось, то гипотеза отклоняется.

Случайную переменную z называют статистикой критерия гипотезы .

Замечание. Описанный алгоритм проверки статистических гипотез допускает возникновение ошибок, т.е. неверных выводов относительно тестируемой гипотезы.

Действительно, гипотеза принимается в качестве истинной с вероятностью . Следовательно, остается вероятность α=1- отвергнуть истинную гипотезу.

При проверке статистических гипотез, связанных с анализом эконометрических моделей, нас будут, в основном, интересовать две искусственно созданные переменные. Это дробь Стьюдента:

(3.1)

и дробь Фишера в виде:

(3.2)

Дробь Стьюдента (3.1) в схеме Гаусса-Маркова имеет закон распределения Стьюдента c параметром 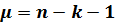. Критическое значение дроби Стьюдента находится из уравнения:

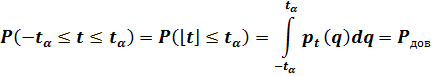
где: α=1-P_дов – вероятность появления ошибки или уровень значимости критерия;

p_t - функция плотности вероятности распределения Стьюдента.

- решение приведенного интегрального уравнения. В математике она называется двусторонней квантилью распределения Стьюдента или критическое значение дроби Стьюдента.

Критическое значение дроби Стьюдента находится по таблице или с помощью функции СТЬЮДРАСПОБР(), в приложении EXCEL. Параметрами этой функции являются уровень значимости (вероятность отклонения гипотезы) α и значение (n-k-1), которое называется степенью свободы.

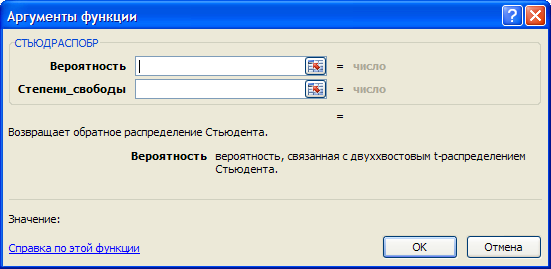
Рис.3.1 Запрос для расчета

Дробь Фишера при условии, что случайные переменные u и v распределены по нормальному закону, подчиняется закону распределения Фишера с параметрами n и m. Критическое значение дроби Фишера есть результат решения уравнения:

Здесь 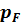- функция плотности вероятностей закона распределения Фишера. 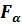- в математике называют односторонней квантилью распределения Фишера или критерием Фишера. Его значение можно также найти в приложении EXCEL с помощью функции FРАСПОБР(). В качестве параметров функции используются уровень значимости критерия (вероятность отклонения гипотезы) α и значения n и m.

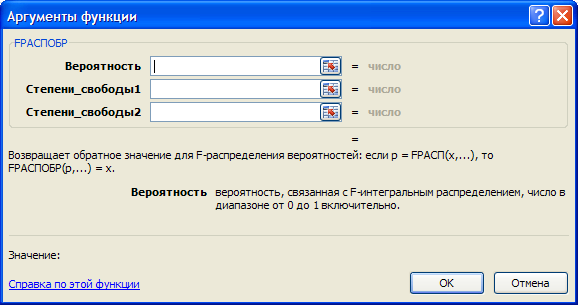
Рис.3.2 Запрос для расчета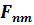

n– степень свободы 1

m – степень свободы 2.

Дата добавления: 2015-10-29