Подведем итог

1. Определены причины и последствия на значения параметров модели при наличии гетероскедастичности случайных возмущений.

2. Сформулирована идея проверки модели на гетероскедастичность случайных возмущений.

3. Рассмотрены алгоритмы тестирования случайных возмущений на гетероскедастичность с помощью теста Голдфельда-Квандта и теста ранговой корреляции Спирмена.

4. Рассмотрен прием устранения гетероскедастичности с помощью весовых функций.

5. Сформулирована теорема взвешенного метода наименьших квадратов.

Вопросы для самоконтроля

1. Дайте определение понятию гомоскедастичности (гетероскедастичности) случайных возмущений.

2. Каковы возможные причины возникновения гетероскедастичности.

3. Каковы последствиягетероскедастичности.

4. В чем идея проверки модели на гомоскедастичность остатков.

5. Опишите алгоритмы тестирования модели на гомоскедастичность с помощью теста Голдфелда-Квандта и теста Спирмена.

6. В чем идея метода устранения гетероскедастичности.

7. Самостоятельно по имеющимся данным провести построение моделей, протестировать их на гомоскедастичность остатков и, в случае необходимости, устранить гетероскедастичность.

8. Сформулируйте теорему взвешенного метода наименьших квадратов.

Лекция 5. Тестирование модели на наличие автокорреляции. Обобщенный метод наименьших квадратов

Содержание лекции

1. Понятие автокорреляции случайных возмущений и авторегрессионной модели.

2. Тест Дарбина-Уотсона.

3. Методы оценки параметров линейной модели в условиях автокорреляции.

4. Обобщенный метод наименьших квадратов.

Продолжаем анализировать оцененную линейную модель на соответствие предпосылкам, изложенным в теореме Гаусса-Маркова. Мы уже рассмотрели методы тестирования второй предпосылки теоремы, а именно, предпосылки о гомоскедастичности случайных возмущений. На очереди третья предпосылка теоремы: предпосылка о независимости случайных наблюдений в уравнениях наблюдений:

(5.1)

Причинами автокорреляции случайных возмущений могут быть следующими:

- ошибки спецификации модели (пропуск важного регрессора, неправильный вид объясняющей части модели);

- ошибки измерения переменных модели;

- характер наблюдений и характер процесса.

Если причиной автокорреляции является ошибка в спецификации модели, то такую автокорреляцию называют ложной.

Автокорреляция чаще всего встречается при анализе данных временного ряда, т.е. в случаях, когда выборка данных имеет упорядоченный вид и при анализе процессов, имеющих циклический характер. Случайное возмущение подвергается воздействию тех переменных, влияющих на эндогенную переменную, которые не включены в спецификацию модели. Если значение случайного наблюдения в любом наблюдении должно быть независимым от его значения в предыдущем наблюдении, то и значение любой переменной, «скрытой» в случайном возмущении, должно быть некоррелированным с ее значением в предыдущих наблюдениях.

Для экономических процессов наиболее типичным является случай положительной автокорреляции. Она является следствием постоянной направленности воздействия тех переменных, которые не вошли в спецификацию модели. Характерным признаком наличия положительной автокорреляции случайных возмущений является периодическое чередование зон с одинаковыми знаками случайного возмущения. Пример модели с положительной автокорреляцией случайных возмущений приведен на рис. 5.1.

Рис. 5.1. Пример диаграммы рассеяния с положительной автокорреляцией случайных возмущений.

Возможен и другой вид автокорреляции – отрицательная автокорреляция рис. 5.2. Характерным признаком наличия отрицательной автокорреляции является пилообразный вид ломаной кривой, соединяющей последовательные наблюдения.

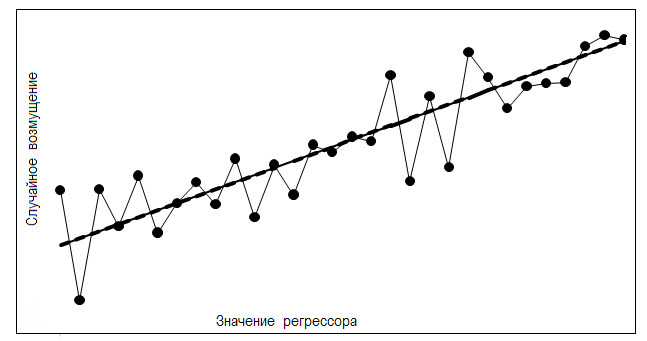
Рис.5.2. Пример диаграммы рассеяния с отрицательной автокорреляцией случайных возмущений.

Возможен и другой вид автокорреляции – отрицательная автокорреляция рис. 5.2.

Модели с автокоррелированными остатками называются авторегрессионными.

В зависимости от глубины взаимного влияния случайных возмущений, рассматривают различные авторегрессионные модели. Например, модель считается авторегрессионной первого порядка AR(1), если взаимосвязь между двумя последовательными случайными возмущениями имеет место соотношение:

В авторегрессионной модели третьего порядка AR(3) случайные возмущения связаны соотношением:

Последствия автокорреляции случайных возмущений в регрессионных моделях сводятся к тому, что стандартная ошибка оценок параметров модели теряет свойство несмещенности. При этом, ее значение, как правило, становится заниженным. Однако оценки параметров остаются несмещенными, т.к. предполагается, что первая предпосылка теоремы Гаусса-Маркова 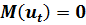в уравнениях наблюдений выполняется.

Тест Дарбина-Уотсона. Данный тест является наиболее часто применяемым для тестирования автокорреляции в регрессионных моделях. Его важность определяется тем, что он позволяет идентифицировать, как ложную, так и истинную автокорреляцию. Этот тест рассматривает наиболее важный, частный случай, третьей предпосылки теоремы Гаусса-Маркова:

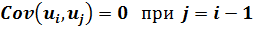
Т.е. рассматривается случай взаимного влияния случайных возмущений в соседних наблюдениях.

В основе теста лежат следующие предположения:

- случайные возмущения подчиняются нормальному закону распределения;

- тип авторегрессии AR(1), т.е. случайные возмущения связаны между собой правилом:

Статистика Дарбина-Уотсона, с помощью которой тестируется модель на автокорреляцию, имеет вид:

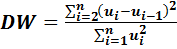(5.2)

Здесь: i – номер наблюдения;

n – количество наблюдений;

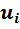- значение случайного возмущения.

Найдем область определения статистики . Раскроем скобки в (5.2):

Принято во внимание, что при достаточно больших значениях n:

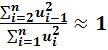, а т.к. , то можно записать:

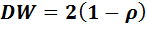(5.3)

Т.к. коэффициент корреляции , то .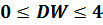

Оказалось, что критическое значение статистики Дарбина-Уотсона зависит не только от значения доверительной вероятности, количества регрессоров в модели и числа наблюдений, но еще и от абсолютных значений регрессоров. Это обстоятельство не дает возможности найти единое для любой модели и любой выборки значение DW_крит. Получается, что в каждом конкретном случае необходимо искать свое значение DW_крит. Это неудобно.

Выяснилось, что возможно найти отрезок [d_L; d_u], внутри которого будут находиться все возможные значения для DW_крит, т.е. .

Тогда для принятия решения относительно наличия или отсутствия автокорреляции можно построить следующую схему. Отложим отрезок [0; 4] и на нем отметим значения d_L, d_u, 4 - d_L; 4-d_u

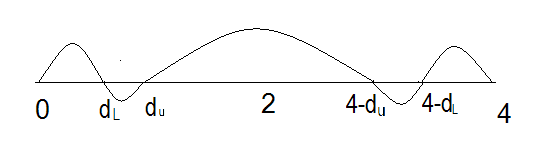
Если реальное значение статистики DW попало на периферийные отрезки [0; d_L] или [4-d_L;4], то гипотеза об отсутствии автокорреляции (выполнении третьей предпосылки теоремы Гаусса-Маркова) отклоняется.

Если реальное значение статистики DW оказалось внутри отрезка [du; 4-du], то гипотеза о выполнении третьей предпосылки теоремы Гаусса-Маркова принимается.

Если реальное значение статистики DW оказалось внутри интервалов [d_L; du] или [4-du; 4-d_L], то определенного вывода сделать нельзя. Эти интервалы называются зонами неопределенности.

Единственный способ раскрыть неопределенность – это воспользоваться другой выборкой. Но мы уже отмечали, что получение дополнительной выборке в экономике дело проблематичное (по времени, стоимости, последствиям). В качестве альтернативной выборки может служить исходная выборка, увеличенная или уменьшенная на одно наблюдение. Альтернативной выборкой может служить исходная выборка с измененной последовательностью наблюдений. Это изменит значение числителя в (5.2), а, следовательно, значение DW. Проследив тенденцию перемещения значений DW вдоль отрезка [0; 4], можно определиться с принятием гипотезы об автокорреляции случайных возмущений.

Алгоритм реализации теста Дарбина – Уотсона можно представить в виде последовательности следующих действий.

Шаг 1. По результатам наблюдений за переменными объекта оценивается модель линейной регрессии.

Шаг 2. Для каждого уравнения наблюдения оценивается значение случайного возмущения.

Замечание. Уравнение линейной регрессии имеет вид:

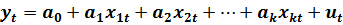
Оценка (прогноз) значений эндогенных переменных в каждом уравнении наблюдения есть:

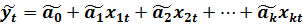
Тогда оценка значения случайного возмущения в наблюдении за номером t равно:

Шаг 3. В соответствующей статистической таблице (см. Приложение 1) по значениям k (число регрессоров в модели) и n (объем выборки) находятся числа d_L и du.

Шаг 4. Проверить на какой отрезок попало вычисленное значение статистики Дарбина-Уотсона.

Пример. Оценить и протестировать на наличие автокорреляции модель величины государственных расходов в зависимости от ВВП.

В таб. 5.1. приведены исходные данные по 34 странам, а также промежуточные результаты анализа модели на автокорреляцию.

Оцененная модель получила вид:

(5.4)

Таб.5.1. Исходные данные для оценки модели (5.4)

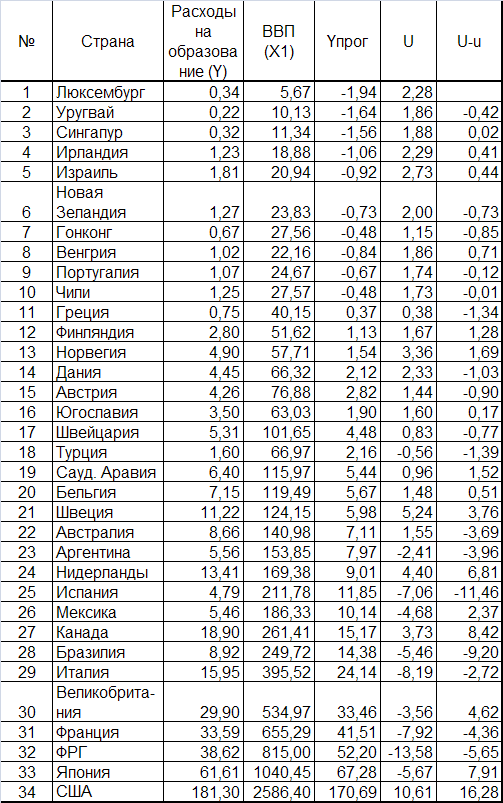
По оцененной модели (5.4) вычислены прогнозные значения расходов на образование (столбец Yпрог) и оценки случайных возмущений в каждом наблюдении.

В последнем столбце таблицы вычислены значения . Расчет производится с i=2. Далее вычисляется

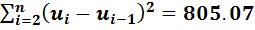, . В результате получаем .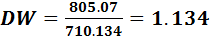

По таблице находим значения d_L =1.39 и du=1.51. Тогда имеем , следовательно, оцененная модель (5.4) является авторегрессионной моделью первого порядка.

В лекции 2 было установлено, что модель (5.4) гетероскедастична и, следовательно, необходимо для оценки использовать взвешенный метод наименьших квадратов.

В таб. 5.2. приведены данные для оценки модели вида:

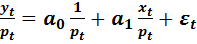(5.5)

Оценка спецификации модели (5.5) имеет вид:

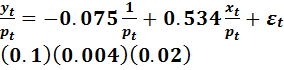(5.6)

При регрессор оказывается статистически незначимый, т.к. дробь Стьюдента для него

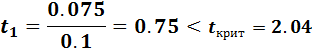
Следовательно, для дальнейшей работы можно ограничиться спецификацией:

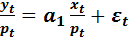(5.7)

Оценка спецификации (5.7) получает вид:

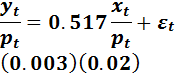
В таб. 5.2. прогнозное значение Y* рассчитано по модели (5.7)

Таб. 5.2. Исходные данные для оценки моделей (5.6) и (5.7)

№	Страна	Y/P	1/P	X/P	Y*	U*	U*-u*
	Люксембург	0,051	0,150	0,850	0,044	0,007
	Уругвай	0,020	0,090	0,910	0,047	-0,027	-0,034
	Сингапур	0,026	0,081	0,919	0,047	-0,022	0,006
	Ирландия	0,062	0,050	0,950	0,049	0,013	0,034
	Израиль	0,082	0,046	0,954	0,049	0,033	0,020
	Новая Зеландия	0,051	0,040	0,960	0,050	0,002	-0,032
	Гонконг	0,023	0,035	0,965	0,050	-0,026	-0,028
	Венгрия	0,044	0,043	0,957	0,049	-0,005	0,021
	Португалия	0,042	0,039	0,961	0,050	-0,008	-0,003
	Чили	0,044	0,035	0,965	0,050	-0,006	0,002
	Греция	0,018	0,024	0,976	0,050	-0,032	-0,026
	Финляндия	0,053	0,019	0,981	0,051	0,003	0,035
	Норвегия	0,083	0,017	0,983	0,051	0,033	0,030
	Дания	0,066	0,015	0,985	0,051	0,015	-0,017
	Австрия	0,055	0,013	0,987	0,051	0,004	-0,012
	Югославия	0,055	0,016	0,984	0,051	0,004	0,000
	Швейцария	0,052	0,010	0,990	0,051	0,001	-0,003
	Турция	0,024	0,015	0,985	0,051	-0,027	-0,028
	Сауд. Аравия	0,055	0,009	0,991	0,051	0,003	0,031
	Бельгия	0,059	0,008	0,992	0,051	0,008	0,005
	Швеция	0,090	0,008	0,992	0,051	0,038	0,030
	Австралия	0,061	0,007	0,993	0,051	0,010	-0,029
	Аргентина	0,036	0,006	0,994	0,051	-0,015	-0,025
	Нидерланды	0,079	0,006	0,994	0,051	0,027	0,043
	Испания	0,023	0,005	0,995	0,051	-0,029	-0,056
	Мексика	0,029	0,005	0,995	0,051	-0,022	0,007
	Канада	0,072	0,004	0,996	0,051	0,021	0,043
	Бразилия	0,036	0,004	0,996	0,051	-0,016	-0,036
	Италия	0,040	0,003	0,997	0,052	-0,011	0,005
	Великобрита-ния	0,056	0,002	0,998	0,052	0,004	0,016
	Франция	0,051	0,002	0,998	0,052	0,000	-0,005
	ФРГ	0,047	0,001	0,999	0,052	-0,004	-0,004
	Япония	0,059	0,001	0,999	0,052	0,008	0,012
	США	0,070	0,000	1,000	0,052	0,018	0,011

Для модели (5.7) получили: ,

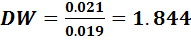, , d_L =1.39 и du=1.51. Реальное значение статистики DW лежит внутри интервала (1.51; 2.0), следовательно, модель (5.7) неавторегрессионная. Третья предпосылка теоремы Гаусса-Маркова принимается истинной с .

Принимая во внимание, что в результате изменения спецификации модели (5.5) удалось устранить автокорреляцию случайных возмущений, следует считать, что автокорреляция в спецификации (5.5) была ложной, т.е. вызвана неудачной записью вида модели.

Оценивание линейных моделей в условиях автокорреляции. Рассмотрим линейную авторегрессионную модель первого порядка AR(1):

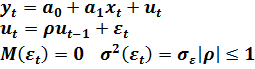(5.8)

Для определенности будем рассматривать пример уравнения парной регрессии. Будем полагать, что коэффициент корреляции между последовательными значениями случайных возмущений 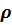известен, а остаток подчиняется нормальному закону распределения . Начальные условия модели определяются нормальной случайной переменной 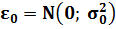. Мы не располагаем нулевым наблюдением, но будем предполагать, что дисперсия случайного наблюдения в нем равна . Тогда из второго уравнения (5.8) получим:

(5.9)

Т.к. и суть независимые случайные переменные, третье слагаемое в (5.9) равно нулю. Поскольку 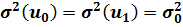, то из (5.9) получаем:

(5.10)

Вычислим дисперсию случайной переменной u_t. Воспользуемся методом математической индукции. Найдем дисперсию u₂:

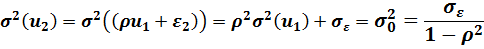
Вычислив значения , и т.д., получим, что во всех случаях:

(5.11)

Таким образом, если задать дисперсию случайного возмущения в начальный момент времени в виде (5.10), то дисперсии во всех наблюдениях станут гомоскедастичными.

Подход к устранению автокорреляции случайных возмущений сводится к искусственному преобразованию спецификации модели (5.8) к виду с тождественным выполнением третьей предпосылки теоремы Гаусса-Маркова.

Для этого запишем первое уравнение (5.8) в моменты времени t и t-1.

(5.12)

Умножим второе уравнение (5.11) на ρ и вычтем его из первого:

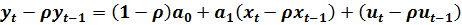(5.13)

Сделав замену переменных:

(5.14)

Получим спецификацию линейной модели вида:

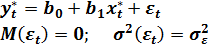(5.15)

Спецификация (5.15) может быть оценена с помощью МНК.

Не нарушая общности полученные выводы можно перенести для линейной модели множественной регрессии.

Уравнения (5.13) имеют смысл только при , т.к. отсутствует нулевое наблюдение. Если объем выборки достаточно велик, то первым наблюдением можно пожертвовать. В принципе первое наблюдение также можно использовать при вычислении оценок модели, если его умножить на величину , которая называется поправкой Прайса-Уинстона. Можно показать, что умножение первого наблюдения на эту поправку не приводит к искажению значений параметров модели и при значениях близких к единице уменьшается значение дисперсии случайного возмущения (5.11).

В результате система уравнений наблюдений принимает вид (5.16):

Замечание. Рассмотренный прием справедлив, если известен коэффициент корреляции между последовательными случайными возмущениями. На практике, как правило, он неизвестен.

При неизвестном значении коэффициента корреляции применяется итерационная процедура метода последовательных приближений. Этот метод получил название процедура Кохрейна-Оркатта.

Алгоритм итерационной процедуры Кохрейна-Оркатта следующий.

Задается число .

1. Значению коэффициента корреляции присваивается значение .

2. По имеющейся выборке оцениваются значения параметров модели и значения случайных возмущений по системе уравнений наблюдений (5.15).

3. По массиву случайных возмущений оценивается модель

4. Получается значение 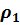, которое сравнивается с предыдущим значением коэффициента корреляции.

5. Если выполняется условие , то процесс поиска параметров прекращается. В противном случае переменной 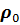присваивается значение 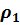, и повторяются шаги 2, 3, 4.

В качестве оценок параметров модели (5.15) и значения коэффициента корреляции принимаются оценки, полученные на последней итерации.

Пример. Исследуется модель, связывающая количество вакансий 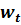и уровень безработицы 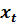. В качестве показателя количества вакансий принято значение

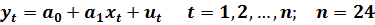
Задание. По данным табл.5.3 оценить спецификацию модели.

Таблица 5.3.

№			№
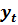
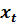
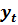
	0,548	2,158		0,802	1,917
	0,663	1,573		0,723	2,110
	1,115	0,982		1,203	1,235
	1,428	0,982		0,751	2,054
	0,924	0,948		1,147	1,552
	0,536	2,088		0,652	2,008
	0,668	2,178		0,815	1,826
	0,944	1,712		1,821	0,971
	1,621	1,054		0,728	2,146
	1,033	1,666		2,127	0,956
	1,488	1,197		1,012	1,833
	1,160	1,694		1,808	0,993

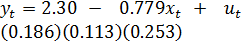
При этом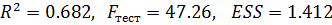

Проверяем качество спецификации. Имеем уравнение парной регрессии, следовательно, достаточно воспользоваться оценкой коэффициента детерминации, 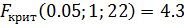, следовательно, модель имеет качественную спецификацию .

Проверяем справедливость третьей предпосылки теоремы Гаусса-Маркова. Вычисляем значение статистики DW. Результаты расчета числителя статистики DW приведены в таб. 5.4.

Таблица 5.4.

№	yt	yt*	ut	(ut-ut-1)^2	№	yt	yt*	ut	(ut-ut-1)^2
	0,548	0,619	-0,071	-		0,802	0,806	-0,004	0,034
	0,663	1,074	-0,412	0,116		0,723	0,656	0,067	0,005
	1,115	1,535	-0,420	0,000		1,203	1,337	-0,134	0,041
	1,428	1,535	-0,107	0,098		0,751	0,699	0,052	0,035
	0,924	1,561	-0,637	0,281		1,147	1,091	0,057	0,000
	0,537	0,673	-0,136	0,251		0,652	0,735	-0,083	0,020
	0,668	0,603	0,065	0,041		0,815	0,877	-0,062	0,000
	0,944	0,966	-0,022	0,008		1,821	1,543	0,278	0,115
	1,621	1,478	0,143	0,027		0,728	0,628	0,100	0,032
	1,033	1,002	0,031	0,013		2,127	1,555	0,572	0,223
	1,488	1,367	0,121	0,008		1,012	0,872	0,140	0,187
	1,160	0,980	0,180	0,003		1,808	1,526	0,282	0,020
								å	1,557

Здесь символом y* обозначено прогнозное значение эндогенной переменной.

Вычисленное значение статистики Дарбина-Уотсона

Выбираем из таблиц Дарбина-Уотсона значения границ критического значения статистики: d_L и d_u (по параметрам: n =24, =1, a=0,05)

d_L =1,273, d_u =1,446

Поскольку d_L — значение статистики попадает в первый интервал, что означает наличие положительной автокорреляции в остатках регрессии. Последствия, к которым приводит автокорреляция, описаны выше. В частности, смещены все оценки ошибок параметров.

Выполним корректировку автокорреляции случайного возмущения методом Кохрейна-Оркатта. Для модель построена, оценки случайных возмущений вычислены, по ним можно оценить модель .

В таб. 5.5. Приведены результаты применения функции «ЛИНЕЙН» к данным таб. 5.4.

Таблица 5.5.

	Н/Д

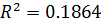
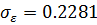
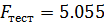
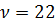
С оценкой выполним преобразования (5.14), и по преобразованным данным оценим модель. Преобразованные данные представлены в таблице 5.6. Примем .

Результаты оценки параметров модели по данным таблицы 5.6 приводятся в таблице 5.7.

Таблица 5.6.

№	yt	xt	№	yt	xt
	0,490964	1,933396		0,28671	1,164499
	0,41957	0,614383		0,366739	1,258439
	0,820485	0,283249		0,881832	0,297706
	0,9327	0,545781		0,216609	1,505394
	0,289661	0,511781		0,813394	0,639582
	0,125545	1,666884		0,142485	1,318578
	0,429901	1,250478		0,525372	0,934016
	0,647264	0,744499		1,458965	0,159863
	1,201661	0,293503		-0,08092	1,714667
	0,312927	1,197797		1,803611	0,002714
	1,029126	0,456937		0,067154	1,40833
	0,499008	1,162274		1,358454	0,178753

Таблица 5.7.

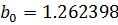
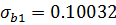
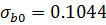
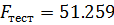
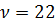
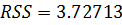
В силу (5.14) оценка параметра может быть непосредственно использована для исходной модели, оценку параметра 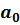нужно вычислить с учетом (5.14):

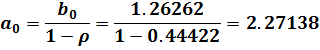
Запишем стандартную форму оцененной модели:

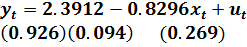(5.17)

Используя результаты оценивания (5.17) снова вычислим остатки и по ним оценку коэффициента корреляции 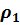. Для итераций i=2, вновь преобразуем выборку в соответствии с (5.14), оцениваем с помощью МНК модель (5.13) и т.д. Результаты этой работы обобщены в таблице 5.8.

Таблица 5.8.

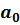
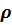
№ итерации					DW
	2.99319	-0.77886		0.44422	1.10176
	2.27138	-0.71826	1.26262	0.444215	2.39938
	2.27137	-0.71827	1.26262	0.444116	2.39926
	2.271.37	-0.71827	1.26263	0.444109	2.39925

Т.к. 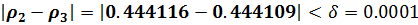, то на третьей итерации процесс можно остановить. При этом случайные возмущения в модели (5.15) попарно не коррелированные, т.к.

Процедура Дарбина. Эта процедура использует спецификацию (5.13). В ней раскрываются скобки, и лаговая переменная y_t-1 включается в число регрессоров:

(5.18)

Введя обозначения: 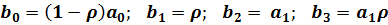, вновь получим спецификацию линейной модели множественной регрессии:

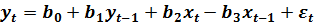(5.19)

Оценив с помощью МНК параметры модели (5.19), можно найти оценки и .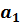

Пример. Оценить спецификацию модели (5.9) по данным таб. 5.3.

В таб. 5.9. приведены исходные данные и элементы расчета статистики Дарбина-Уотсона.

Таблица 5.9.

№	yt	yt-1	xt	xt-1	ut	ut-ut-1
	0,548		2,158
	0,663	0,548	1,573	2,158	-0,43964
	1,115	0,663	0,982	1,573	-0,25254	0,187094
	1,428	1,115	0,982	0,982	0,118455	0,370997
	0,924	1,428	0,948	0,982	-0,54939	-0,66784
	0,536	0,924	2,088	0,948	0,200058	0,749445
	0,668	0,536	2,178	2,088	0,079725	-0,12033
	0,944	0,668	1,712	2,178	-0,10978	-0,1895
	1,621	0,944	1,054	1,712	0,127359	0,237138
	1,033	1,621	1,666	1,054	0,012274	-0,11509
	1,488	1,033	1,197	1,666	0,088504	0,07623
	1,16	1,488	1,694	1,197	0,15774	0,069236
	0,802	1,16	1,917	1,694	-0,09534	-0,25308
	0,723	0,802	2,11	1,917	0,038531	0,13387
	1,203	0,723	1,235	2,11	-0,22293	-0,26146
	0,751	1,203	2,054	1,235	0,141898	0,364828
	1,147	0,751	1,552	2,054	-0,01606	-0,15796
	0,652	1,147	2,008	1,552	-0,10618	-0,09012
	0,815	0,652	1,826	2,008	-0,06799	0,038192
	1,821	0,815	0,971	1,826	0,268775	0,336767
	0,728	1,821	2,146	0,971	0,035582	-0,23319
	2,127	0,728	0,956	2,146	0,462493	0,42691
	1,012	2,127	1,833	0,956	-0,05552	-0,51801
	1,808	1,012	0,993	1,833	0,183973	0,23949

Результат оценки модели с помощью функции «ЛИНЕЙН» имеет вид:

0,432726	-0,79144	0,437487	1,174001
0,191566	0,113946	0,211814	0,517995
0,735104	0,240758	#Н/Д	#Н/Д
17,5754		#Н/Д	#Н/Д
3,056254	1,101327	#Н/Д	#Н/Д

Следовательно,

; ;

Значение статистики DW=2.092, что свидетельствует об отсутствии автокорреляции между случайными возмущениями.

Отметим, что при использовании процедуры Дарбина, пришлось «пожертвовать» первым наблюдением, чего мы не делали в предыдущем примере.

Как видно, получены результаты достаточно хорошо коррелированные с результатами, полученными с помощью процедуры Кохрейна-Оркатта.

Обобщенный метод наименьших квадратов. Обобщим рассмотренные способы устранения гетероскедастичности и автокорреляции в линейных моделях множественной регрессии.

Вновь обратимся к ковариационной матрице случайных возмущений.

В случае, когда вторая и третья предпосылки в уравнениях наблюдений нарушены, ее можно записать в виде:

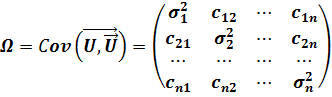(5.20)

На главной диагонали матрицы (5.20) расположены дисперсии случайных возмущений, которые в общем случае, могут быть неоднородными. На боковых местах лежат значения ковариаций c_ij=Cov(u_i,u_j). Доказана теорема, которая формулирует наилучшую линейную процедуру оценки параметров линейной модели множественной регрессии в случае, если ковариационная матрица случайных возмущений имеет вид (5.20), т.е. в условиях, когда вторая и третья предпосылки теоремы Гаусса-Маркова не выполняются.

Теорема Эйткена. В классе линейных несмещенных оценок вектора параметров линейной модели множественной регрессии, , наилучшей является оценка:

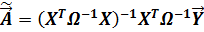(5.21)

Процедура (5.21) называется обобщенным методом наименьших квадратов. От классического метода наименьших квадратов он отличается тем, что оценки параметров находятся из условия минимальности функционала:

Если матрица Ω диагональная (c_ij=0), то процедура (5.21) соответствует взвешенному методу наименьших квадратов (ВМНК). Если в матрице Ω на главной диагонали лежат нули, то процедура (5.21) обеспечивает получение наилучших оценок в условиях автокорреляции случайных возмущений при выполнении условия гомоскедастичности. Если матрица Ω диагональная и все 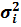равны, то процедура (5.21) превращается в процедуру классического метода наименьших квадратов (МНК).

В заключении отметим, что применение ОМНК требует знания ковариационной матрицы вектора случайных возмущений Ω, что встречается крайне редко. На практике используется, так называемый, доступный обобщенный метод наименьших квадратов. К нему относят те процедуры, которые мы рассмотрели выше – это ВМНК и процедуры устранения автокорреляции.

---

Дата добавления: 2015-10-29