Использование табличного процессора EXCEL для оценки параметров регрессионных линейных моделей

Отметим, что современный уровень развития и доступность вычислительной техники вызвали потребность к разработке различных пакетов прикладных программ для ПЭВМ, позволяющих упростить процесс вычислений. Статистические расчеты были одной из первых областей применения средств ЭВТ. В настоящее время существует достаточно большой набор программных продуктов, ориентированных на решение задач эконометрики. Это E-VIEWS, STATA и др. Как правило, это дорогостоящие программные продукты, которые, далеко не всегда, доступны для использования. Поэтому мы воспользуемся доступным, практически каждому, пакетом Микрософт-офис и в частности программой EXCEL.

В этом приложении есть несколько функций, которыми можно воспользоваться для построения и последующего анализа эконометрических моделей. Мы рассмотрим наиболее простую, а именно, функцию «ЛИНЕЙН».

Рассмотрим применение этой функции в виде последовательности действий специалиста.

Первое. Работа начинается с того, что на рабочем листе создается набор данных, т.е. вводится содержимое выборки наблюдений за поведением объекта. Это таблица, содержащая значения эндогенной и экзогенных переменных.

На рис. 2.1 приведен фрагмент рабочего листа с данными для оценивания линейной модели «Затраты на еду в зависимости от располагаемого дохода и численности семьи». Отметим, что считается хорошим тоном сопровождать непосредственные числовые данные поясняющими комментариями. Так на рис.2.1 в качестве комментариев используется «шапка» таблицы и столбец «А», «Номер наблюдения по порядку».

Рис. 2.1 Фрагмент рабочего листа EXCEL

Второе. На листе выделяется область высотой в пять строк и шириной равной количеству столбцов с данными. В данном примере их три. Столбец «Номер по порядку» содержит комментарий. При массивах данных небольшого размера рекомендуется выделять эту область непосредственно под данными.

Третье. Вызывается функция «ЛИНЕЙН». Чтобы это сделать, достаточно с помощью «мышки» нажать на экране кнопку . На экране появится запрос на выбор функции Рис.2.2.

Если функция «ЛИНЕЙН» ранее использовалась, она появится в списке, если нет, в «черном прямоугольнике» необходимо ввести слово «ЛИНЕЙН» и нажать кнопку «Найти», функция появится в списке.

Выделив функцию, необходимо нажать кнопку «ОК» и функция «ЛИНЕЙН» откликнется запросом на ввод исходной информации Рис. 2.3.

Рис. 2.1. Фрагмент рабочего листа.

Рис. 2.2. Запрос на вызов функции.

Программа просит указать, в каких ячейках расположены значения эндогенной переменной (y), указать расположение экзогенных переменных. В нашем примере это (x₁, x₂). В соответствующих окнах появятся «адреса» расположения соответствующих массивов.

Необходимо дополнительно ввести значения двух констант: «Конст» и «Статистика». С помощью первой константы программе сообщается присутствует (1) или нет (0) в спецификации модели свободный параметр 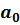. Второй константе «Статистика» присваивается значение «1». Это означает, что Вы хотите получить полную информацию, которую может предоставить функция «ЛИНЕЙН».

Четвертое. Для завершения процесса ввода исходной информации необходимо набрать на клавиатуре комбинацию клавиш «Cntr+Shift+Enter».

Внимание. Здесь чаще всего встречаются ошибки. Необходимость набора данной комбинации диктуется требованием EXCEL при работе с массивами данных.

После этого функция «ЛИНЕЙН» заполнит выделенную ранее область на листе следующими данными Таб. 2.1.

Рис. 2.3. Запрос исходной информации.

R^2		н/д
Fтест	(n-k-1)	н/д
RSS	ESS	н/д

Таб. 2.1. Результаты работы функции «ЛИНЕЙН»

Обсудим содержимое результирующей таблицы. В первой строке, справа налево, расположены оценки параметров модели. Во второй, под оценками параметров, расположены оценки стандартных ошибок соответствующих параметров. Далее заполняются только два левых столбца. В таб. 2.1 приведены обозначения соответствующих величин. Их смысл и названия будем раскрывать по мере использования. Сейчас назовем - ошибка случайного возмущения. Для приведенного на рисунках примера результат выглядит следующим образом:

Рис. 2.4. Результат работы функции «ЛИНЕЙН»

Согласно полученным результатам модель следует записать в следующем виде:

На этом завершаем обсуждение задачи построения модели.

Но с учетом изложенного необходимо заметить, что в задачу третьего этапа построения модели необходимо дополнительно включить необходимость проведения анализа полученных результатов на выполнение предпосылок теоремы Гаусса-Маркова.

---

Дата добавления: 2015-10-29