Теорема Гаусса-Маркова

Вопрос. Почему оказались важными свойства оценок? Это связано с тем, что при моделировании реальных объектов, в том числе экономических, параметры являются не только числовыми коэффициентами при переменных, а несут на себе смысловую нагрузку, имеют размерность и по их величинам делают вывод о свойствах объекта.

Например. Если модель (2.8) описывает зависимость расходов на потребление от располагаемого дохода, то параметр 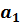есть предельные расходы по доходу и показывает, на сколько единиц изменяются расходы на потребление при увеличении дохода на одну единицу.

Теорема Гаусса-Маркова формулирует условия, при которых МНК позволяет получить наилучшие оценки параметров линейной модели множественной регрессии.

Не смотря на огромную разницу в возрасте ученых, теорема получила название по их именам. Гаусс – английский ученый, Марков – российский. Заслуга Гаусса в разработке МНК, заслуга Маркова в формулировке условий, при которых МНК позволяет получить состоятельные оценки.

Сформулируем постановку задачи. Имеем:

- спецификацию модели в виде линейного уравнения множественной регрессии:

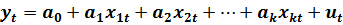(2.17)

- выборку из n наблюдений за поведением переменных модели:

(2.18)

Значения переменных в каждом наблюдении связаны между собой по правилу (2.17). Следовательно, в соответствие каждому наблюдению можно поставить уравнение:

Андрей Андреевич Марков Время жизни 14.06.1856 - 20.07.1922 Научная сфера - математика

Карл Фридрих Гаусс Время жизни: 30.04.1777 – 23.02.1855 Научная сфера – математика, физика, астрономия

(2.19)

Система уравнений (2.19) называется системой уравнений наблюдения или схемой Гаусса-Маркова.

В компактной записи эта система имеет вид:

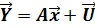
Далее будем использовать следующие обозначения.

- вектор наблюдений за эндогенной переменной:

- вектор параметров линейной модели;

вектор случайных возмущений в уравнениях наблюдений;  

-

матрица коэффициентов при параметрах в системе уравнений наблюдений

-.

В матрице X в первом столбце записана единица. Это «псевдопеременная» при параметре 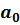. Эта единица появляется в матрице X только в тех случаях, когда спецификация модели содержит свободный параметр 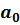. Если на этапе спецификации этот параметр не был записан, то и матрице X столбец из единиц отсутствует.

Найти:

1. Значения состоятельных оценок параметров модели (2.17);

2. Значения несмещенных ошибок оценок параметров;

3. Оценку ошибки случайного возмущения;

4. Оценку наилучшего прогноза с помощью модели (2.17);

5. Оценку ошибки прогноза.

Формулировку теоремы сделаем в виде описания ее содержания.

Теорему условно можно разбить на две части: «если» и «тогда».

Теорема начинается с описания условий, которые накладываются на вектор случайных возмущений. Эти условия принято называть предпосылками теоремы Гаусса-Маркова.

И так. Если

1. Математическое ожидание случайных возмущений во всех наблюдениях равно нулю:

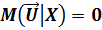(2.20)

2. Дисперсия случайных возмущений во всех наблюдениях одинакова и равна константе σ_u

(2.21)

3. Ковариация между парами случайных возмущений в наблюдениях равны нулю (случайные возмущения в наблюдениях независимы)

(2.22)

4. Ковариация между вектором регрессоров и вектором случайных переменных равна нулю (регрессоры и случайные возмущения независимы)

(2.23)

Тогда. Если матрица X неколлинеарная (нет ни одного столбца, который можно было бы представить в виде линейной комбинации других его столбцов)

1. Наилучшая оценка вектора параметров линейной модели множественной регрессии вычисляется, как

(2.24)

Она соответствует методу наименьших квадратов.

2. Ковариационная матрица оценок параметров модели вычисляется, как:

(2.25)

3. Дисперсия случайного возмущения равна:

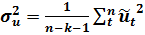(2.26)

4. Наилучший прогноз по модели (2.17) в точке вычисляется по правилу:

(2.27)

5. Ошибка прогноза эндогенной переменной равна:

(2.28)

Учитывая важность теоремы Гаусса-Маркова для эконометрики, рассмотрим ее доказательство.

Доказательство. Воспользуемся методом наименьших квадратов:

(2.29)

где: (2.30)

Подставляя (2.31) в (2.30) и выполнив перемножения, получим:

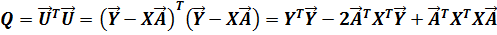(2.31)

Для получения необходимого условия экстремума дифференцируем (2.32) по вектору :

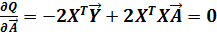(2.32)

Отсюда, система нормальных уравнений для вычисления оценок вектора имеет вид:

(2.33)

Тогда оценка вектора есть:

Выражение (2.24) доказано.

Покажем, что процедура (2.24) дает несмещенную оценку параметров модели множественной регрессии. Для этого необходимо вычислить математическое ожидание вектора оценки :

Таким образом, несмещенность оценки (2.24) доказана. Отметим, что несмещенность достигнута в силу выполнения первой предпосылки теоремы Гаусса-Маркова.

Аналогичным образом доказывается справедливость выражения (2.25).

Замечание. Свойство случайных возмущений (2.21), сформулированное во второй предпосылке теоремы, называется свойством гомоскедастичности случайных возмущений, или свойством однородности дисперсий случайных возмущений или свойством одинаковости дисперсий случайных возмущений во всех наблюдениях.

Свойство (2.22) называют отсутствием автоковариации случайных возмущений.

Вернемся к задаче оценки параметров уравнения парной регрессии и решим ее с помощью процедур, сформулированных в теореме Гаусса-Маркова.

Имеем. Уравнение парной линейной регрессии.

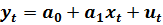(2.34)

Выборку наблюдений объемом n за поведением экономического объекта.

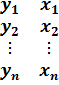(2.35)

Сформируем необходимые вектора и матрицу коэффициентов уравнений наблюдений:

- вектор наблюдений за эндогенной переменной;

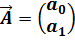- вектор параметров линейной модели;

матрица коэффициентов при параметрах в системе уравнений наблюдений

-.

Столбец из единиц появился в матрице, в связи с тем, что в спецификации (2.34) присутствует параметр .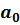

вектор случайных возмущений в уравнениях наблюдений;  

-

Вот все необходимое для оценки модели (2.34).

Выражение (2.24) позволяет вычислить оценки параметров. Для этого вначале вычисляется произведение матриц:

(2.36)

Матрица обратная к (2.37) есть:

(2.37)

Вычисляется произведение:

(2.38)

Подставляя (2.37) и (2.38) в (2.24), получим вектор оценок параметров линейной модели парной регрессии (2.34):

Сравнив полученные выражения с (2.12), убеждаемся в идентичности.

Найдем стандартные ошибки оценок параметров. Для этого воспользуемся выражением (2.25), имея в виду, что на диагонали ковариационной матрицы расположены искомые дисперсии.

(2.39)

Следовательно, дисперсии параметров модели парной регрессии можно вычислить по формулам:

(2.40)

(2.41)

Прогноз в точке вычисляется по формуле (2.27). Осталось найти ошибку прогнозного значения . Эта ошибка вычисляется по формуле (2.28). Для ее применения необходимо вычислить второе слагаемое подкоренного выражения. Обратная матрица известна (2.38). Осталось умножить на нее вначале транспонированный вектор x, а затем просто вектор x.

В итоге получается выражение для в виде:

Окончательно выражение (2.29) принимает вид:

(2.42)

Из выражения (2.42) следует:

1. Минимальное значение ошибка прогнозирования принимает в центре области наблюдаемых значений регрессора, при 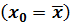и растет в квадратичной зависимости с удалением от центра;

2. Значение ошибки падает с ростом объема выборки.

Прогнозирование по линейным моделям за пределы выборки может

приводить к значительным погрешностям.

В результате мы убедились, что процедура оценки модели, сформулированная в теореме Гаусса-Маркова, поставляет МНК-оценки параметров модели линейной регрессии.

Обсудим вопрос практического использования МНК с помощью персонального компьютера.

---

Дата добавления: 2015-10-29