Лекция 6. Тестирование оцененной модели на адекватность

Содержание лекции:

1. Точечный и интервальный прогноз по регрессионной модели.

2. Понятие адекватности модели.

3. Алгоритм проверки модели на адекватность.

4. Точечный и интервальный методы проверки модели на адекватность.

На сегодня Вы уже знаете, как записать спецификацию линейной модели, как собрать и представить для расчетов выборку результатов наблюдения за поведением экономического объекта, процедуру МНК для идентификации модели, порядок тестирования идентифицированной модели на качество спецификации, тестирование на выполнение предпосылок теоремы Гаусса-Маркова о гомоскедастичности и отсутствии автокоррелируемости случайных возмущений, знакомы с доступными обобщенными методами устранения гетероскедастичности и автокорреляции.

Осталась четвертая предпосылка теоремы Гаусса-Маркова, об отсутствии корреляции между векторами регрессоров и случайных возмущений. Если эта предпосылка не выполняется, то это приводит к смещению МНК-оценок параметров модели. Это было установлено на лекции 2, когда рассматривали механизм работы метода наименьших квадратов.

При построении линейных моделей, в которых значения регрессоров в каждом наблюдении являются константами, четвертая предпосылка выполняется автоматически, т.к. связь между константой и случайной величиной всегда отсутствует. Предполагается, что зафиксировав выборку наблюдений, зафиксировали и значения регрессоров в каждом наблюдении и, следовательно, исключили связь между векторами регрессоров и случайных возмущений. Поэтому нет необходимости в дополнительном тестировании последней предпосылки теоремы Гаусса-Маркова.

Заметим, что такое положение далеко не всегда имеет место. Например, если значения регрессоров в каждом наблюдении суть результат измерений, то связь между векторами регрессоров и случайных возмущений может иметь место, т.к. измерения всегда производятся с некоторой ошибкой, а это означает, что результаты измерений являются случайными величинами. Следовательно, возможна и связь регрессоров со случайными возмущениями. Второй пример. В качестве регрессора может выступать лаговая эндогенная переменная, значение которой сформировалось в предшествующий момент времени. Лаговая эндогенная переменная является случайной величиной, т.к. на ее формирование оказало влияние соответствующее случайное возмущение. Опять в составе регрессоров оказалась случайная переменная, которая может взаимодействовать со случайным возмущением.

Рассмотрение перечисленных ситуаций выходит за рамки изучаемого курса. Забегая вперед, отметим, что возникновение таких ситуаций существенно осложняет возможность получения состоятельных оценок параметров линейной модели.

В результате мы подошли к последнему этапу построения модели, а именно, этапу проверки адекватности модели.

Проверка адекватности тесно связана с прогнозированием с помощью построенной модели. Поэтому начнем с рассмотрения вопроса получения наилучшего прогноза с помощью линейной регрессионной модели.

Прогнозирование с помощью регрессионной модели. В теореме Гаусса-Маркова сформулировано правило получения наилучшего прогноза по линейной модели в точке :

(6.1)

Для получения прогнозного значения эндогенной переменной в некоторой точке достаточно в спецификации модели заменить символическое обозначение параметров значениями оценок этих параметров с помощью МНК. Естественно, что точка не принадлежит выборке наблюдений. Нет никакого практического смысла прогнозировать уже известное из практики значение эндогенной переменной. Исключения составляют случаи проверки статистических гипотез, статистики которых содержат оценки значений случайных возмущений (например, статистика DW).

Замечание. В (6.1) отсутствует значение случайного возмущения, которое присутствовало в спецификации модели.

Это объясняется тем, что мы не можем значение случайного возмущения ни наблюдать, ни прогнозировать. Случайное возмущение появилось в спецификации модели с целью обеспечения однозначной связи между эндогенной переменной и регрессорами. По (6.1) вычисляется оценка математического ожидания (среднего значения) эндогенной переменной, в котором отсутствует случайное возмущение в силу первой предпосылки теоремы Гаусса-Маркова.

Однако, оценка среднего значения есть величина случайная, которое вычисляется с некоторой ошибкой. Следовательно, значение, вычисленное по (6.1) необходимо дополнить значением оценки стандартной ошибки прогнозирования.

Теорема Гаусса-Маркова дает ответ на вопрос, как вычисляется ошибка прогнозирования:

(6.2)

Здесь: - стандартная ошибка случайных возмущений;

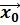- точка, в которой оценивается прогнозное значение;

- матрица коэффициентов системы уравнений наблюдений.

Таким образом, с помощью (6.1) и (6.2) имеется возможность вычислить в интересующей нас точке среднее значение эндогенной переменной и значение ее стандартной ошибки.

Такой способ прогнозирования иногда называют точечным.

На практике чаще применяют интервальный метод прогнозирования. Его идея заключается в том, чтобы оценить числовой интервал, в котором с заданной доверительной вероятностью могут лежать реальные значения эндогенной переменной. Для вычисления границ этого интервала, который принято называть доверительным, воспользуемся статистикой Стьюдента t для оценки модуля разности между прогнозным и реальным значением эндогенной переменной:

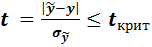(6.3)

Здесь: – прогнозное значение эндогенной переменной в интересующей точке;

- ожидаемое значение эндогенной переменной в той же точке;

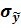- значение стандартной ошибки прогноза в той же точке;

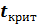- Критическое значение дроби Стьюдента при заданном значении доверительной вероятности (значимости) и известном значении ν=n-k-1.

Решив неравенство (6.3) относительно y, получим:

(6.4)

Из (6.4) видно, что ожидаемое значение эндогенной переменной в

заданной точке с вероятностью может принять любое значение внутри интервала

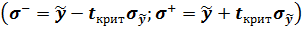(6.5)

Имея границы доверительного интервала, легко оценить множество возможных значений, которые может принять эндогенная переменная с известной доверительной вероятностью.

Пример. Построить линейную модель зависимости объема внутреннего национального продукта (y) от объема национального потребления (с) и объема инвестиций (I) и оценить возможный объем ВНП, если объем потребления достигнет уровня c=14.5 млрд.долл, а объем инвестиций I=4.0 млрд.долл.

Исходные данные для построения модели приведены в таб. 6.1

Таблица 6.1.

№ п/п	y (млрд.долл)	С (млрд.долл)	I (млрд.долл)
			1,65
		9,5	1,8
			2,1
			2,2
	23,5		2,4
			2,65
	26,5	16,5	2,85
	28,5		3,2
	30,5		3,55

Модель, оцененная по данным таб. 6.1, имеет вид:

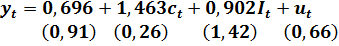(6.6)

Опустим необходимый анализ модели и перейдем к оценке прогнозного значения ВНП при заданных значениях объема потребления (c=14.5) и объема инвестиций I=4.0. Воспользовавшись результатом (6.6), вычислим среднее значение ВНП в заданных условиях:

(6.7)

Дополнительно необходимо вычислить оценку стандартной ошибки в точке прогнозирования. Чтобы воспользоваться (6.2), необходимо сформировать матрицу X коэффициентов уравнений наблюдений.

Замечание. Пользуясь функцией «ЛИНЕЙН», табличного процессора EXCEL, нам не приходилось формировать матрицу X. Достаточно было присвоить переменной «Константа» значение один или ноль и функция «ЛИНЕЙН» сама выполняла необходимые преобразования. На этапе прогнозирования и проверки адекватности модели создавать матрицу X придется самостоятельно.

В данном примере матрица X имеет вид:

(6.8)

Вектор x₀ примет вид: .

Замечание. Единицы в первом столбце матрицы X и единица в векторе x₀ появились в связи с тем, что в спецификации модели присутствует параметр a₀. В случаях, когда параметр a₀ отсутствует в спецификации модели, в матрице X и векторе x₀ отсутствуют соответственно столбец из единиц и единица.

Значение константы q в (6.2) удобно вычислять в два этапа. На первом этапе вычислить матрицу . Она не зависит от точки прогнозирования. Затем вычислить значение q для точки прогнозирования при известной матрице .

Последовательность операций при вычислении обратной матрицы с помощью процессора EXCEL следующая:

1. На листе EXCEL выделяется область, в которую предполагается поместить матрицу .

2. Набирается следующая командная строка:

После чего последовательно нажимается комбинация клавиш . Выделенная область будет заполнена числовыми значениями матрицы .

[X] – означает протянуть область, занимаемую матрицей X.

Замечание. Напоминаю, что матрица квадратная, размерность которой равна количеству столбцов в матрице X.

Для вычисления значения константы q достаточно позиционировать курсор в выбранной ячейке и набрать командную строку:

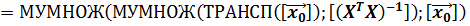
В выделенной ячейке появится значение константы q.

Для данного примера имеем:

q=8,74;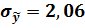

В результате точечный прогноз имеет вид

Найдем границы доверительного интервала возможных значений эндогенной переменной для P_дов=0,95 (α=0,05, t_крит=2,36):

Следовательно, в данном примере ожидаемые значения объема ВНП может принять любое значение из интервала (23,74; 26,86).

Оценка адекватности модели. Начнем с определения адекватности.

Определение. Под адекватностью понимается возможность получения результата с удовлетворительной точностью.

Эконометрические модели создаются для последующего их использования как инструмент прогнозирования поведения эндогенной переменной экономического объекта в различных условиях. Или, другими словами, ответить на вопрос, что будет, если предопределенные переменные объекта примут некоторое значение. Модель служит инструментом имитации поведения экономического объекта в различных ситуациях. Понятно, что лучшим ответом на вопрос, “что будет?”, было бы наблюдение за объектом в интересующей ситуации. Однако, в экономике это или не возможно, или чревато необратимыми негативными последствиями.

Следовательно, в нашем случае под адекватностью модели следует понимать возможность получения прогноза с удовлетворительной точностью.

Очевидно, чтобы оценить точность прогноза, необходимо сопоставить вычисленное по модели прогнозное значение эндогенной переменной с ее реальным значением при одинаковых значениях набора регрессоров.

Если разница между этими значениями по абсолютной величине окажется приемлемой, то можно будет сделать вывод об адекватном описании поведения объекта полученной моделью.

Поняв идею тестирования, рассмотрим алгоритм ее реализации.

Шаг 1. Имеющаяся выборка делится на две неравные части. Первая объемом 5% - 10% от общего объема выборки, вторая – все остальное. Первую выборку называют контрольной, вторую – обучающей. Из названия понятно, что первая (маленькая) выборка предназначена для тестирования модели на адекватность, вторая (большая) предназначена для оценивания модели. Необходимость выделения из общего объема контрольной выборки связано с тем, что необходимо обеспечить независимость значений оценок параметров от влияния элементов контрольной выборки. В противном случае тест становится некорректным, т.к. тестирование на адекватность модели проводится по тем же данным, по которым осуществляется идентификация модели.

Возникает вопрос, в какой момент необходимо провести деление выборки, в самом начале работы или непосредственно перед проведением тестирования. В общем случае не имеет значения. Однако, на практике при принятии решения определяющее значение играет объем выборки. Если объем выборки достаточно большой, (например, n>100), то поделить выборку можно сразу. Если объем выборки относительно небольшой, то это делать рекомендуется непосредственно перед тестированием на адекватность, т.к. заметное уменьшение выборки может существенно сказаться на значениях оценок параметров, их ошибках и, как следствие, привести к искаженным результатам по всем тестам, которые необходимо провести в процессе построения модели.

Шаг 2. По обучающей выборке вновь проводится идентификация модели.

В связи с тем, что изменилась выборка, по которой производится оценка модели, изменятся и значения оценок параметров модели.

Шаг.3. Используя полученные значения оценок параметров модели, вычисляются значения оценок эндогенной переменной для каждой точки контрольной выборки.

Шаг 4. Формулируется статистическая гипотеза о равенстве реального и прогнозного значений эндогенной переменной в каждой точке контрольной выборки: .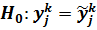

Индекс k указывает на принадлежность контрольной выборке, индекс j порядковый номер точки в контрольной выборке.

Для тестирования выдвинутой гипотезы используется критерий Стьюдента

(6.9)

Для использования критерия Стьюдента необходимо дополнительно вычислить оценку среднего квадратичного отклонения прогнозного значения эндогенной переменной в каждой точке контрольной выборки (6.2).

Шаг 5. Вычисляются значения дроби Стьюдента и проверяется выполнение условия (6.9).

Если условие (6.9) выполняется в каждой точке контрольной выборки, то делается вывод об адекватности модели с доверительной вероятностью .

Выполнение условия (6.9) можно проверить интервальным способом. Для этого необходимо вычислить границы доверительного интервала (6.5).

Если реальное значение эндогенной переменной лежит в границах доверительного интервала (говорят, доверительный интервал накрывает реальное значение), то модель в данной точке адекватна. Если это справедливо для всех точек контрольной выборки, то гипотеза об адекватности модели принимается с вероятностью .

Пример. Проверить адекватность модели (6.6).

Шаг 1. Формируем контрольную и обучающую выборки.

Выберем для проверки адекватности две точки: точку с номером 2 и точку с номером 10.

Шаг 2. Оцениваем модель по обучающей выборке.

Шаг 3. Вычисляется оценка эндогенной переменной в каждой точке выборки.

Шаг 4. Вычисляется оценка стандартной ошибки в каждой точке контрольной выборки.

Шаг 5. Вычисляются значения статистик Стьюдента или границы доверительных интервалов для каждой контрольной точки, и проверяется условие принятия гипотезы об адекватности.

Результаты перечисленных процедур приведены в таб. 6.2.

Таблица 6.2.

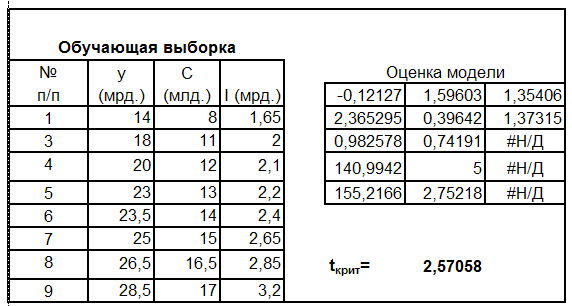
Статистическая гипотеза об адекватности модели (6.6) принимается с вероятностью 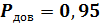. Это подтверждают результаты тестирования, как с помощью дроби Стьюдента, так и с помощью доверительных интервалов.

Мы рассмотрели последний этап построения эконометрических моделей, на основании которого делается вывод о возможности использования построенной модели для решения задач оптимального управления.

В заключении рассмотрим пример построения эконометрической модели, подобную той, которая будет предложена в качестве экзаменационной.

Задача. Построить эконометрическую модель зависимости объема продаж (y) от следующих факторов:

x₁ – результат теста способностей;

x₂ – возраст продавца;

x₃ – результат теста на тревожность;

x₄ – стаж работы по специальности;

x₅ – средний балл школьного аттестата.

Решение.

1. Спецификация модели имеет вид:

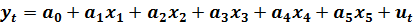(6.10)

2. Выборка результатов наблюдения за экономическим объектом приведена в таб. 6.3.

3. Вычисляются оценки параметров модели (6.10) с помощью функции «ЛИНЕЙН»

Таблица данных, которая генерируется функцией «ЛИНЕЙН» представлена в таб. 6.4.

Оценка модели (6.10) по данным таб. 6.3. имеет вид:

4. Анализ модели на качество спецификации.

Значение коэффициента детерминации R²=0.89, статистика F_тест =38.64, (см. таб. 6.4.) F_крит(0.05; 5; 23)=2.64. Следовательно, выбранные регрессоры в целом оказывают значимое влияние на формирование эндогенной переменной.

Таблица 6.3.

№ П/П	y	x1	x2	x3	x4	x5
		19,0	22,5	3,0	1,0	2,6
		27,0	23,1	1,5	0,0	2,8
		31,0	24,0	0,6	3,0	2,7
		64,0	22,6	1,8	2,0	2,0
		81,0	21,7	3,3	1,0	2,5
		42,0	23,8	3,2	0,0	2,5
		67,0	22,0	2,1	0,0	2,3
		48,0	22,4	6,0	1,0	2,8
		64,0	22,6	1,8	1,0	3,4
		57,0	21,1	3,8	0,0	3,0
		10,0	22,5	4,5	1,0	2,7
		48,0	22,2	4,5	0,0	2,8
		96,0	24,8	0,1	3,0	3,8
		75,0	22,6	0,9	0,0	3,7
		12,0	20,5	4,8	0,0	2,1
		47,0	21,9	2,3	1,0	1,8
		20,0	20,5	3,0	2,0	1,5
		73,0	20,8	0,3	2,0	1,9
		4,0	20,0	2,7	0,0	2,2
		9,0	23,3	4,4	1,0	2,8
		98,0	21,3	3,9	1,0	2,9
		27,0	22,9	1,4	2,0	3,2
		59,0	22,3	2,7	1,0	2,4
		23,0	22,6	2,7	1,0	2,4
		90,0	22,4	2,2	2,0	2,6
		34,0	23,8	0,7	1,0	3,4
		16,0	20,6	3,0	1,0	2,3
		32,0	24,4	0,6	3,0	4,0
		94,0	25,0	4,6	5,0	3,6

Оценим статистическую значимость влияния на эндогенную переменную каждого из факторов.

Таблица 6.4.

-0,56687	-0,07518	0,190797	6,203462	0,199641	-91,6779
1,766074	0,800749	0,521451	0,935023	0,028722	18,12653
0,893624	4,014295	#Н/Д	#Н/Д	#Н/Д	#Н/Д
38,64295		#Н/Д	#Н/Д	#Н/Д	#Н/Д
3113,572	370,635	#Н/Д	#Н/Д	#Н/Д	#Н/Д

Для этого необходимо проверить выполнение гипотезы о равенстве нулю параметров при каждом регрессоре. Вычислим значения дроби Стьюдента и найдем значение t_крит.

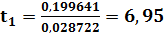
Сравнив значения t -статистик с критическим, делаем вывод о том, что гипотеза 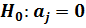принимается для j=3, 4, 5. Следовательно, три последних регрессора не оказывают с вероятностью 0,95 статистически значимого влияния на формирование эндогенной переменной. Это значит, что их можно исключить из спецификации (6.10).

Это, в свою очередь, означает возврат к этапу спецификации модели. Новая спецификация принимает вид:

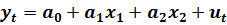(6.11)

В результате тестирования качества спецификации модели, последняя была существенно упрощена. С экономической точки зрения это означает, что на объеме продаж сказываются только способности и возраст продавца.

Для оценки спецификации (6.11) вновь готовим выборку результатов наблюдений. Эта работа сводится к тому, что из дальнейшего рассмотрения исключаются три последних столбца таб. 6.3.

Таблица 6.5.

№ П/П	y	x1	x2
1,0	30,0	4,0	20,0
2,0	58,0	9,0	23,3
3,0	47,0	10,0	22,5
4,0	33,0	12,0	20,5
5,0	39,0	16,0	20,6		5,934158	0,196058	-86,6
6,0	39,0	20,0	20,5		0,565995	0,025508	12,49643
7,0	47,0	19,0	22,5		0,892464	3,796146	#Н/Д
8,0	49,0	23,0	22,6		107,8894		#Н/Д
9,0	52,0	27,0	22,9		3109,528	374,6789	#Н/Д
10,0	60,0	27,0	23,1		Fкрит=	3,369016
11,0	71,0	31,0	24,0		t2	t1
12,0	62,0	32,0	24,4		10,48447	7,686123
13,0	61,0	34,0	23,8		tкрит=	2,055529
14,0	58,0	42,0	23,8
15,0	54,0	47,0	21,9
16,0	53,0	48,0	22,2
17,0	66,0	48,0	22,4
18,0	51,0	57,0	21,1
19,0	56,0	59,0	22,3
20,0	61,0	64,0	22,6
21,0	61,0	64,0	22,6
22,0	56,0	67,0	22,0
23,0	52,0	73,0	20,8
24,0	65,0	75,0	22,6
25,0	60,0	81,0	21,7
26,0	63,0	90,0	22,4
27,0	78,0	94,0	25,0
28,0	59,0	98,0	21,3
29,0	74,0	96,0	24,8

Оцениваем спецификацию модели (6.11), и убеждаемся в ее качестве (см. таб. 6.5.).

Оцененная модель имеет вид:

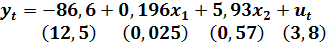(6.12)

Переходим к тестированию модели (6.12) на гомоскедастичность случайных возмущений.

Согласно порядку применения теста Голдфельда-Квандта, вводим служебную переменную , сортируем выборку по возрастанию переменной 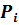, делим выборку на три части и вычисляем значения статистик GQ₁ и GQ₂.

Результаты вычислений приведены в таб. 6.6. Из приведенных данных видно, что статистическая гипотеза о постоянстве дисперсии случайных возмущений отвергается исходными данными с вероятностью 0,95.

Вывод. Необходимо принимать меры по устранению гетероскедастичности случайных возмущений.

Воспользуемся взвешенным методом наименьших квадратов. Вводим весовую функцию 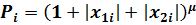, принимаем начальное значение показателя степени μ=1, вновь возвращаемся к этапу спецификации модели.

Приводим спецификацию модели к виду:

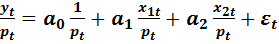(6.13)

Для оценки спецификации (6.13) необходимо подготовить выборку наблюдений, затем идентифицировать модель, проверить ее качество спецификации и убедиться в ее гомоскедастичности или гетероскедастичности.

В таб.6.7. Приведены данные и результаты расчета статистики Голдфельда-Квандта для μ=1.

Таблица 6.6.

№ П/П	y	x1	x2	P
		96,0	24,8	0,021
		98,0	21,3	0,022
		94,0	25,0	0,022
		90,0	22,4	0,023
		81,0	21,7	0,024		Оценка моделей
		75,0	22,6	0,025
		73,0	20,8	0,026			0,134	-60,7
		67,0	22,0	0,027		0,46	0,047	9,633
		64,0	22,6	0,028		0,96	1,742	#Н/Д
		64,0	22,6	0,028		87,6		#Н/Д
		59,0	22,3	0,029			21,24	#Н/Д
		57,0	21,1	0,030
		48,0	22,4	0,033
		48,0	22,2	0,033		6,99	0,162	-110
		47,0	21,9	0,033		0,96	0,156	19,92
		42,0	23,8	0,035		0,92	3,295	#Н/Д
		34,0	23,8	0,038		38,2		#Н/Д
		32,0	24,4	0,039			75,99	#Н/Д
		31,0	24,0	0,040
		27,0	23,1	0,043
		27,0	22,9	0,043		GQ1=	0,279
		23,0	22,6	0,046		GQ2=	3,578
		19,0	22,5	0,050		Fкрит=	2,978
		20,0	20,5	0,051
		16,0	20,6	0,055
		10,0	22,5	0,060
		12,0	20,5	0,060
		9,0	23,3	0,061
		4,0	20,0	0,076

Как видно из таб. 6.7. при μ=1 модель (6.13) остается гетероскедастичной. Необходимо подобрать показатель степени μ весовой функции, при котором условие гомоскедастичности случайных возмущений будет выполняться тождественно.

Таблица 6.7.(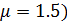

№ П/П	Y/P	1/P	X1/P	x2/P
	1,200	0,040	0,160	0,800
	1,742	0,030	0,270	0,700
	1,403	0,030	0,299	0,672
	0,985	0,030	0,358	0,612
	1,037	0,027	0,426	0,548
	0,940	0,024	0,482	0,494
	1,106	0,024	0,447	0,529
	1,052	0,021	0,494	0,485		Оценка "верхней" модели
	1,022	0,020	0,530	0,450		7,225679	0,146093	-114,914
	1,174	0,020	0,528	0,452		0,817031	0,142737	16,83772
	1,268	0,018	0,554	0,429		0,99676	0,080849	#Н/Д
	1,080	0,017	0,557	0,425		717,8474		#Н/Д
	1,037	0,017	0,578	0,405		14,07664	0,045756	#Н/Д
	0,868	0,015	0,629	0,356
	0,773	0,014	0,672	0,313		Оценка "нижней" модели
	0,744	0,014	0,674	0,312		5,078488	0,13888	-62,9035
	0,924	0,014	0,672	0,314		0,505501	0,047432	10,67389
	0,645	0,013	0,721	0,267		0,999454	0,017142	#Н/Д
	0,680	0,012	0,717	0,271		4271,816		#Н/Д
	0,696	0,011	0,731	0,258		3,765927	0,002057	#Н/Д
	0,696	0,011	0,731	0,258
	0,622	0,011	0,744	0,244
	0,549	0,011	0,770	0,219		GQ1=	22,24373
	0,659	0,010	0,761	0,229		GQ2=	0,044956
	0,579	0,010	0,781	0,209		Fкрит=	3,443357
	0,556	0,009	0,794	0,198
	0,650	0,008	0,783	0,208
	0,490	0,008	0,815	0,177
	0,608	0,008	0,788	0,204

Результаты расчетов при различных значениях показателя степени весовой функции приведены таб. 6.8. Как видно из таб.6.8., увеличение показателя степени μ приводит к усилению степени гетероскедастичности. Модель становится гомоскедастичной с вероятностью 0,95 при μ=-0,8.

Таблица 6.8.

	GQ1	GQ2	Fкрит
μ=1	22,244	0,045	2,9782
μ=2	146,6	0,0068
μ=0	3,5779	0,2795
μ=-0,8	0,947	1,152

Следующий шаг – проверка полученной модели на отсутствие автокорреляции случайных возмущений.

В таб. 6.9. приведены результаты расчета статистики Дарбина – Уотсона. Как видно, полученная модель не автокоррелированная. Значение статистики DW находится в интервале между D_u и 2.

Остается последний этап: проверка адекватности модели.

Разбиваем имеющуюся выборку таб. 6.9. В контрольную выборку включим три точки. Пусть это будут затененные в таб. 6.9.точки. Эти точки выбраны исходя из принципа наибольших по абсолютной величине случайных возмущений.

Оценка модели (6.13) по данным обучающей выборки имеет вид:

(6.14)

Для реализации теста необходимо вычислить значения q, и прогнозных значений переменной в каждой точке контрольной выборки.

Матрица коэффициентов X и результаты расчетов матрицы и значений константы q приведены в таб. 6.10., а результат тестирования модели на адекватность в таб 6.11.

Таблица 6.9.

Y/P	1/P	X1/P	x2/P	Yпрог	u	ui-ui-1
393,98	13,13	52,53	262,65	471,94	-77,96
958,04	16,52	148,66	384,87	890,57	67,47	145,43
780,07	16,60	165,97	373,44	828,99	-48,92	-116,39
547,71	16,60	199,17	340,24	662,89	-115,18	-66,26
709,93	18,20	291,25	374,99	749,33	-39,40	75,78
768,25	19,70	393,97	403,82	814,59	-46,34	-6,95
943,65	20,08	381,47	451,75	1034,74	-91,10	-44,75
1059,02	21,61	497,09	488,45	1140,32	-81,30	9,80
1206,08	23,19	626,24	531,14	1276,18	-70,10	11,20
1396,01	23,27	628,20	537,46	1304,30	91,71	161,81
1777,50	25,04	776,09	600,84	1537,84	239,65	147,94
1583,15	25,53	817,11	623,04	1625,95	-42,80	-282,45
1587,93	26,03	885,08	619,55	1585,87	2,06	44,86
1672,05	28,83	1210,79	686,12	1796,99	-124,94	-126,99
1614,27	29,89	1405,01	654,68	1595,55	18,72	143,66
1607,90	30,34	1456,21	673,50	1671,75	-63,85	-82,57
2006,79	30,41	1459,49	681,09	1707,01	299,78	363,63
1683,11	33,00	1881,12	696,34	1682,95	0,15	-299,63
1907,69	34,07	2009,89	759,67	1961,01	-53,32	-53,48
2184,40	35,81	2291,83	809,30	2148,68	35,72	89,04
2184,40	35,81	2291,83	809,30	2148,68	35,72	0,00
2049,19	36,59	2451,71	805,04	2101,29	-52,10	-87,83
1983,58	38,15	2784,64	793,43	1993,76	-10,18	41,93
2558,67	39,36	2952,32	889,63	2438,42	120,26	130,43
2459,09	40,98	3319,77	889,37	2391,14	67,95	-52,31
2773,52	44,02	3962,17	986,14	2798,08	-24,56	-92,51
3592,85	46,06	4329,85	1151,56	3580,60	12,26	36,82
2723,11	46,15	4523,12	983,09	2735,67	-12,56	-24,82
3449,45	46,61	4474,96	1156,03	3591,67	-142,22	-129,66
5,18	0,18	-68,38	0,00	Σ(ui-ui-1)^2=	509900,3
0,48	0,02	10,73	#Н/Д
1,00	103,00	#Н/Д	#Н/Д		DW=	1,84861
3301,50	26,00	#Н/Д	#Н/Д		DL	1,21
1,1E+08		#Н/Д	#Н/Д		DU	1,65

Отметим, что в матрице X отсутствует столбец из единиц. Это явилось следствием отсутствия свободного коэффициента в модели (6.14).

В контрольных векторах экзогенных переменных по той же причине отсутствуют единицы.

Таблица 6.10

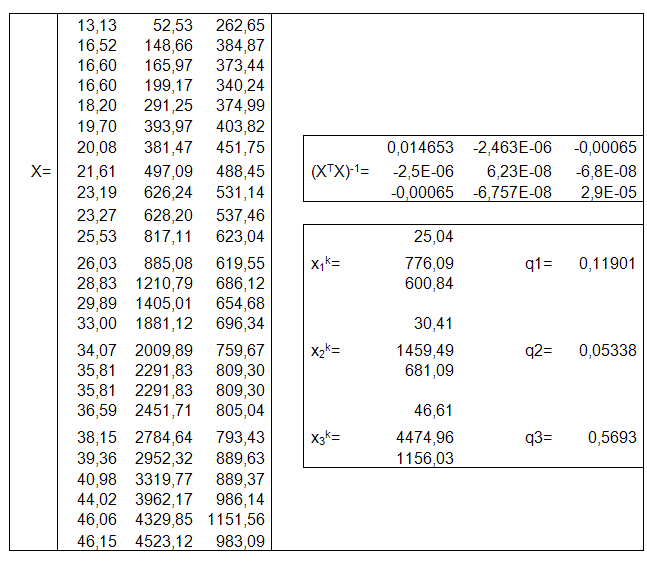
Таблица 6.11.

Y/P	1/P	X1/P	x2/P	y	q	sigma	t
1777,50	25,04	776,09	600,84	1509,92	0,119	65,638	4,08
2006,79	30,41	1459,49	681,09	1683,06	0,0534	63,684	5,08
3449,45	46,61	4474,96	1156,03	3642,49	0,5693	77,73	2,48

Учитывая, что значение t_крит(0,05; 22)=2,074, модель следует считать не адекватной, т.к. во всей контрольной выборке условие 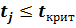не выполняется.

Дата добавления: 2015-10-29