Анализ модели фирмы

Статика модели

Производственная деятельность фирмы

- К началу 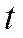- периода

- Выручка за 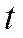- период

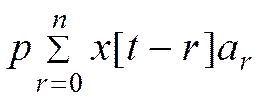- выручка от реализации в конце 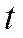- периода

- затраты

(8)

В течение периодов фирма выпускает один и тот же объем продукции 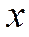, т.е. ,

,

(9)

,

(10)

Выпуск - точка безубыточности.

(11)

(11а)

Динамика модели

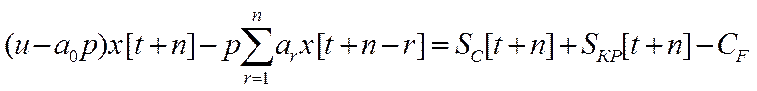
(12)

Общее решение уравнения (12) применительно к экономическим системам можно назвать реакцией фирмы , под которой понимается последовательность выпусков при имеющихся финансовых средствах.

Оно включает две составляющие: , называемое свободной составляющей реакции, и 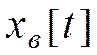– вынужденная составляющая реакции.

Однородное линейное разностное уравнение

(13)

Общее решение уравнения (13) ищется в следующей последовательности:

- составляется характеристическое уравнение на основание (13)

;

- находятся корни этого уравнения ;

- записывается общее решение (13) в форме

где - независимое частное решение однородного уравнения (13), соответствующее корню характеристического уравнения .

Частное решение неоднородного уравнения часто удается найти по правой части уравнения (12).

Пример. Рассмотрим простой случай, когда продукция полностью реализуется в течение текущего и прошлого периодов, т.е. , и , . Тогда уравнение (12) с начальными условиями принимает вид

, (14)

где .

Полагая правую часть (14), равной нулю, получаем однородное разностное уравнение

,

на основание которого составляем характеристическое уравнение

.

Это уравнение имеет один вещественный корень

,

которому соответствует частное решение , определяющее свободную составляющую реакции фирмы

.

Структура частного решения неоднородного разностного уравнения (14) определяется его правой частью, представляющей собой полином нулевого порядка, , где неизвестная величина. Подставляя решение 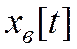в уравнение (14)

,

находим вынужденную составляющую реакции

.

Общее решение уравнения (14) имеет вид

.

Для решения задачи Коши составляем и решаем уравнение относительно величины с

.

Записываем решение задачи Коши (реакцию фирмы)

. (15)

Поставим задачу: организовать выпуск продукции и привлечение кредитов в таком объеме, чтобы к концу планируемого периода достичь желаемого объема производства и вернуть кредиты вместе с процентами.

Обозначим через - производственную мощность фирмы;

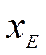- емкость рынка, характеризующую возможность полной реализации продукции фирмы;

- желаемый объем производства к концу планового периода;

- срок, на который берутся кредиты;

- ставка кредита;

Целевая функция, определяющая желаемый выпуск в

конце планового периода

(16)

В первом периоде выпуск определяется размером взятого кредита исходя из условия баланса (4)

(17)

В следующем периоде фирма берет новый кредит и возвращает часть ранее взятого вместе с процентами

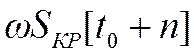
(18)

За периодов до конца планового интервала прекращается привлечение кредитов и производится возвращение займов и процентов по ним. Это делается для того, чтобы к концу планового периода фирма не имела невозвращенных кредитов и процентов по ним.

Linprog

[x,fval]=linprog(-f,A,b,[],[],lb,ub)

Данная модель описывает, в частности, задачу линейного программирования, решением которой являются последовательность выпусков и поток кредитов , которые максимизируют целевую функцию при заданных ограничениях. В принципе, могут быть и другие варианты построения оптимизационной модели, в которой, например, функциональные ограничения могут быть заданы в виде неравенств.

Дата добавления: 2015-10-23