Алгоритм модели

Схема теплообменника

Условные обозначения

Исходные данные к расчету теплообменного аппарата:

Наименование параметра	Единица измерения	Условное обозна- чение
Массовый расход горячего потока (теплоносителя)	кг/ч	gh *
Массовый расход холодного потока (нагреваемого продукта)	кг/ч	gc *
Относительный удельный вес: горячего потока	безразм.	dh
холодного потока	безразм.	dc
Начальная температура: горячего потока	°C	tnh *
холодного потока	°C	tnc *
Конечная температура горячего потока	°C	tkh *
Внутренний диаметр: внутренней трубы	мм	dv *
наружной трубы	мм	dn *
Толщина стенки трубы	мм	tt *
КПД теплообменника	безразм.	kpd
Средняя т-рная поправка удельного веса на 1°C: для горячего потока	1/°C	ah
для холодного потока	1/°C	ac
Значения вязкости для соответствующих им температур [два значения при двух температурах]: для горячего потока	°C см^2/с	t1h, t2h v1h, v2h
для холодного потока	°C см^2/с	t1c, t2c v1c, v2c

Примечание. В графе "Условное обозначение" звездочкой помечены параметры, которые можно использовать в качестве варьируемых при исследовании статических характеристик.

Алгоритм модели

Алгоритм модели представлен в двух вариантах: упрощенной блок – схемой (Приложение А) и в виде математических формул, порядок выполнения которых описывается ниже.

Определяются удельные теплосодержания потоков (ккал/кг) при заданных температурах tnh, tkh и tnc:

(5)

По аналогии находятся qkh и qnc.

Из уравнения теплового баланса (с учетом потерь через кпд аппарата) вычисляется удельное теплосодержание холодного потока на выходе из теплообменника:

(6)

Полученное значение qkc записывается в виде формулы (5), из которой конечная температура холодного потока находится как корень квадратного уравнения и равна

, (7)

где

(8)

Рассчитываются среднелогарифмические температуры горячего и холодного потоков:

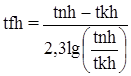, (9)

(10)

Затем при среднелогарифмических температурах потоков находятся их плотности

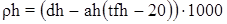, (11)

; (12)

вязкости по формуле Гросса

, (13)

, (14)

где

, (15)

; (16)

средние удельные теплоемкости по формуле Крэга

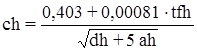, (17)

; (18)

коэффициенты теплопроводности потоков по формуле Крэга

, (19)

; (20)

критерии подобия Рейнольдса

, (21)

; (22)

критерии подобия Прандтля

, (23)

; (24)

критерий подобия Нуссельта для холодного потока

(25)

Коэффициенты теплоотдачи потоков рассчитываются при условии, что их критерии Re>10000 и Pr от 0,7 до 2500:

, (26)

(27)

Это позволяет найти коэффициент теплопередачи

(28)

Далее определяются разности температур потоков на входе и выходе из теплообменника:

, (29)

(30)

При

, (31)

иначе

(32)

Вычисляется количество переданного тепла

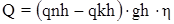, (33)

при котором поверхность теплообмена

, (34)

а полезная длина внутренней трубы составит

(35)

В случае моделирования режимов работы аппарата с целью построения статических характеристик задается начальное значение одного из входных – варьируемых параметров, шаг варьирования и количество точек. Параметры, которые могут быть варьируемыми, обозначены в п. 4.3 знаком «*».

Дата добавления: 2015-10-26