Вторая характерная проблема - это проблема авторегрессионности поведенческих уравнений модели.

Эта проблема тесно связана с четвертой предпосылкой теоремы Гаусса-Маркова: отсутствие связи между регрессорами уравнения и случайными возмущениями.

Получение состоятельных оценок параметров уравнения с помощью МНК удается за счет значительного увеличения объема выборки только в случае:

В случае, когда

получение состоятельных оценок с помощью МНК не возможно.

Именно эта ситуация оказывается типичной для структурных поведенческих уравнений модели.

В качестве иллюстрации рассмотрим элементарную макроэкономическую модель Кейнса. Она имеет спецификацию вида:

(9.19)

здесь: - объем потребления;

– внутренний национальный доход;

- объем внешних инвестиций.

В поведенческом уравнении модели (9.19) в качестве регрессора выступает текущая эндогенная переменная , которая связана с текущим случайным возмущением .

Для того, чтобы в этом убедиться перепишем первое уравнение модели (9.18) в приведенной форме:

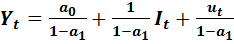(9.20)

Из (9.20) видно, что связано функционально со случайным возмущением , при этом

(9.21)

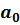Отсюда видно, что , а, следовательно, для первого уравнения модели (9.19) четвертая предпосылка теоремы Гаусса-Маркова нарушается в каждом уравнении наблюдения и не зависит от объема выборки. Следовательно, МНК даст смещенные оценки параметров и .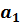

Для того, чтобы понять, в каких случаях с помощью МНК можно получить состоятельные оценки параметров модели в условиях нарушения четвертой предпосылки теоремы Гаусса- Маркова, найдем зависимость оценок параметров от объема выборки. Для этого воспользуемся процедурой МНК, сформулированной в теореме Гаусса-Маркова, умножив и разделив ее выражение на n:

(9.22)

В результате получается выражение для вектора оценок параметров модели:

(9.23)

Второе слагаемое в выражении (9.23) делает оценку вектора параметров модели смещенной, если оно не является нулевым вектором. Именно это слагаемое не позволяет получить состоятельную оценку вектора параметров модели с помощью МНК.

Вместе с тем, выражение (9.23) позволяет сформулировать условия, при которых оценка вектора параметров стала состоятельной при неограниченном увеличении объема выборки. Очевидно, что для этого второе слагаемое в (9.23) должно быть нулевым вектором. Множитель матрица не нулевая, следовательно, нулевым должен быть вектор . Отсюда получаются достаточные условия состоятельности МНК-оценок параметров модели:

1. Существует и равен нулю предел по вероятности:

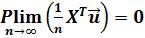(9.24)

2. Существует матрица:

(9.25)

3. Справедливо равенство:

(9.26)

Выполнение условий (9.24) - (9.26) обеспечивает получение состоятельных МНК-оценок параметров линейной множественной регрессии в условиях нарушения четвертой предпосылки теоремы Гаусса-Маркова.

Существуют несколько методов вычисления состоятельных оценок параметров линейной модели множественной регрессии в условиях нарушения четвертой предпосылки теоремы Гаусса-Маркова.

Мы остановимся на методе применения инструментальных переменных как наиболее практичного.

В основе метода лежит понятие инструментальной переменной.

Определение. Пусть имеется модель линейной множественной регрессии

(9.27)

в котором объясняющие переменные коррелируют в пределе со случайными возмущениями (т.е. не выполняется условие (9.24)). Переменные называются инструментальными для модели (9.27), если они удовлетворяют двум требованиям:

1. Существует предел

(9.28)

2. Существует невырожденная матрица:

(9.29)

Из определения следует, что инструментальные переменные в пределе коррелируют с исходными регрессорами , но не коррелируют в пределе со случайными возмущениями. Заметим, что Z и Х матрицы размерностью составленные по результатам наблюдений за соответствующими переменными.

Оставим на время открытым вопрос как подобрать такие переменные, но отметим, что с их помощью удается получить состоятельные оценки параметров линейной модели множественной регрессии с помощью следующей процедуры.

Теорема. Процедура

(9.30)

Доставляет состоятельные оценки параметров модели (9.27).

И так, мы познакомились с проблемами типичными для моделей в виде систем одновременных уравнений и с методами их преодоления.

Перейдем к рассмотрению методов идентификации поведенческих уравнений модели в их структурной форме. Мы остановимся на двух методах – это косвенный метод наименьших квадратов (КМНК) и двухшаговый метод наименьших квадратов (ДМНК).

Косвенный метод наименьших квадратов применим только для точно идентифицируемых уравнений модели. В этом заключается его ограниченность. Алгоритм применения КМНК следующий.

1. Модель записывается в приведенной форме:

Матрица M коэффициентов приведенной формы модели связана с матрицами A и B структурной формы соотношением:

(9.31)

После умножения (9.30) на матрицу A получим:

С использованием расширенной матрицы коэффициентов модели последнее выражение можно записать в виде:

(9.32)

где I единичная матрица, а многоточие означает объединение матриц M и I.

Из (9.32) с учетом априорных ограничений и условия нормализации получается система алгебраических уравнений для расчета значений оценок параметров i -го уравнения модели:

(9.33)

Можно доказать, что, если i -ое уравнение модели точно идентифицируемо и выполнено условие нормализации, система (9.32) имеет единственное решение и доставляет состоятельные оценки структурной формы уравнения.

Заметим, что оценки структурной формы уравнения модели вычисляются косвенно через МНК-оценки параметров приведенной формы этого уравнения. Отсюда и название метода.

Пример. Оценить модель потребления свинины на душу населения (в фунтах) в зависимости от цены на нее (долл/фунт), располагаемого дохода потребителей (долл) и цены на ее переработку 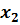(% от цены).

Известны следующие закономерности:

1. Объем потребления свинины зависит от ее цены и располагаемого дохода.

2. Цена на свинину растет с ростом ее потребления и цены на переработку.

Решение.

Шаг 1. С учетом сформулированных закономерностей спецификация модели имеет вид:

(9.34)

В системе (9.34) две текущие эндогенные переменные и три текущие экзогенные переменные

Шаг 2. С помощью правила ранга и правила порядка проверяем идентифицируемость уравнений модели.

Расширенная матрица коэффициентов модели (9.34) и априорные ограничения на ее уравнения имеют вид:

(9.35)

Для первого уравнения (9.34) получим:

1. Правило ранга

2. Правило порядка при K=3, K₁=2, G₁=2

K-K₁=3-2=G₁-1=2-1

Вывод: первое уравнение модели (9.34) точно идентифицированное.

Аналогично проверяем второе уравнение модели (9.34).

1. Правило ранга:

2. Правило порядка при K=3, K₁=2, G₁=2 также выполняется точно.

Следовательно, оба уравнения модели (9.34) точно идентифицированные и для получения состоятельных оценок параметров их структурной формы можно воспользоваться КМНК.

Шаг 2. Оценка параметров приведенной формы модели (9.34).

Приведенную форму модели в общем виде можно записать так:

(9.36)

Значения оценок параметров приведенной формы модели (9.36) можно оценить классическим МНК, применив его к каждому из уравнений (9.36).

Выборка результатов наблюдений за переменными объекта приведена в таб. 9.1.

Таблица 9.1.

В результате в приведенной форме модель принимает вид:

Шаг 3. Составляем систему алгебраических уравнений (9.33) для вычисления значений оценок параметров структурной формы модели (9.34).

Для первого уравнения:

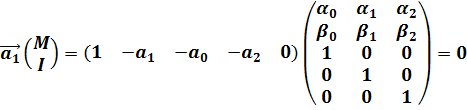(9.37)

Выполнив перемножение в (9.36), получим систему линейных уравнений относительно неизвестных параметров структурной формы первого уравнения:

(9.38)

Решив систему уравнений (9.37) относительно неизвестных оценок параметров, и, подставив в (9.37) значения вычисленных оценок параметров приведенной формы модели, получим:

Аналогичным образом вычисляются оценки параметров структурной формы второго уравнения:

Система алгебраических уравнений есть:

Решение системы уравнений:

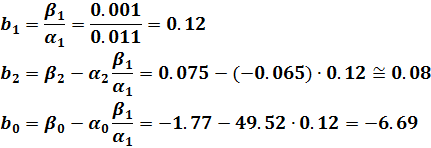
Оцененная модель (9.33) принимает вид:

Отметим, что вычисленные оценки параметров модели (9.34) остаются несмещенными и эффективными при условии, что для уравнений привнений приведенной формы выполняются все предпосылки теоремы Гаусса-Маркова. В этом случае параметры структурной формы модели представляют собой линейную комбинацию несмещенных оценок приведенной формы.

---

Дата добавления: 2015-10-29