Начнем с формулировки необходимого и достаточного условия идентифицируемости уравнений модели.

Для того, чтобы сформулировать соответствующую теорему, вспомним общий вид структурной формы уравнения в системе линейных одновременных уравнений и дадим несколько дополнительных определений.

Общий вид структурной формы уравнения модели имеет вид:

(9.5)

Здесь символами 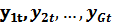обозначены текущие эндогенные переменные, символами 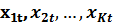предопределенные переменные. (При наличии в уравнениях модели свободных коэффициентов то считается, что предопределенная переменная ) Набор текущих эндогенных и предопределенных переменных описывают в каждый момент времени состояние изучаемого объекта, а случайные возмущения 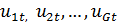отражают воздействие на текущие эндогенные переменные не идентифицированных факторов и индивидуальные особенности объекта. Отметим, что среди уравнений модели могут быть тождества, которые не содержат неизвестных параметров, а случайное возмущение в них равно нулю.

Вспомним (Лекция 1), что в компактной форме модель в виде системы одновременных уравнений можно записать в виде:

(9.6)

где: A – квадратная матрица размерностью коэффициентов, стоящих в уравнениях (9.5) при текущих эндогенных переменных;

В – прямоугольная матрица размерностью 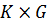коэффициентов, стоящих в уравнениях (9.5) при предопределенных переменных;

- вектор текущих эндогенных переменных;

- вектор предопределенных переменных;

- вектор случайных возмущений.

Введем еще одно предположение: будем считать, что i-ое поведенческое уравнение может быть разрешено относительно i-ой текущей эндогенной переменной, при этом

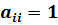(9.7)

Равенство (9.7) называют условием нормализации.Отметим, что для поведенческих уравнений это условие, как правило, выполняется автоматически.

Обозначим символом расширенную матрицу системы одновременных уравнений, которая определяется следующим образом:

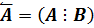(9.8)

Расширенная матрица представляет собой объединение матриц А и В. Она содержит G строк и K+G столбцов. Каждую строку расширенной матрицы можно представить в виде вектора

(9.9)

Определение. Ограничениями на коэффициенты i-го уравнения модели (9.6) называется система из L_i однородных алгебраических уравнений:

, (9.10)

которым априори удовлетворяет вектор .

На практике матрица ограничений строится достаточно просто. Пример. Найти ограничения на уравнения паутинной модели конкурентного рынка.

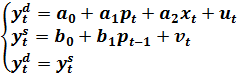(9.11)

В этой модели три текущих эндогенных переменных и три предопределенных переменных . Для первого уравнения модели (9.10) компонентами вектора являются: .Тогда вектор имеет вид:

(9.12)

Тогда в соответствие вектору (9.12) можно поставить два линейных ограничения в виде:

(9.13)

Легко убедиться, что условие (9.10) априори выполняется:

Имея вектор , ограничения к нему строятся очень просто: нужно в строках на месте ненулевых компонент поставить нули, а на месте нулевых компонент поставить единицу. Количество ограничений равно количеству нулевых компонент в векторе .

Теперь можно сформулировать теорему.

Теорема. (Правило ранга) i-ое уравнение модели в виде системы линейных одновременных уравнений идентифицируемо тогда и только тогда, когда справедливо равенство:

(9.14)

где: - ранг произведения матриц .

Пример. Выяснить какое из поведенческих уравнений модели (9.3) является идентифицируемым, а какое нет.

(9.3)

Расширенная матрица этой модели имеет вид:

(9.15)

Ограничениями для векторов поведенческих уравнений модели являются:

(9.16)

(9.17)

Оценим идентифицируемость первого уравнения модели (9.3) с помощью правила ранга.

Т.к. , делаем вывод о неидентифицируемости первого уравнения модели (9.3).

Для второго уравнения получим:

Для второго уравнения модели (9.3) правило ранга выполняется, следовательно, оно является идентифицируемым.

Рассмотрим еще одну теорему, которая оказывается полезной не только при выявлении неидентифицируемых уравнений модели, но имеет также важное самостоятельное значение при выборе метода оценки параметров структурной формы уравнений модели.

Эта теорема получила название правила порядка и формулирует необходимое условие идентифицируемости уравнения модели.

Теорема. Если i-ое уравнение модели в виде системы линейных уравнений идентифицировано, тогда справедливо неравенство:

(9.18)

где: K – общее количество предопределенных переменных в модели;

- количество предопределенных переменных, входящих в i-ое

уравнение модели;

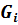- количество текущих эндогенных переменных, входящих в i-ое

уравнение модели.

Неравенство (9.18) говорит о том, что в идентифицированном уравнении модели количество не входящих в i-ое уравнение предопределенных переменных, по крайней мере, на единицу больше количества текущих эндогенных переменных, входящих в это уравнение.

Неравенство (9.18) является необходимым условием идентифицируемости модели. Это означает, что, если модель идентифицируема, то (9.18) выполняется обязательно. Обратное не верно: если (9.18) имеет место, то это не означает, что уравнение следует считать идентифицируемым.

Условием (9.18) пользуются для нахождения неидентифицируемых уравнений модели, рассуждая от противного: если (9.18) не выполняется, то данное уравнение не идентифицированное.

Выражения (9.18) служит еще для классификации уравнений модели в виде системы одновременных линейных уравнений, разделяя их на точно идентифицируемые и сверх идентифицируемые.

Для точно идентифицируемых уравнений модели выполняются следующие условия:

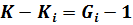
Для сверх идентифицируемых уравнений имеет место:

Выполнение правила ранга обеспечивает идентифицируемость уравнения модели, а с помощью правила порядка относят это уравнение к тому или другому классу.

Закончили обсуждение первой проблемы оценки параметров структурной формы уравнений в модели в виде системы одновременных уравнений.

Дата добавления: 2015-10-29