Лекция 8. Построение нелинейных моделей

Содержание лекции:

1. Типы нелинейных моделей, поддающихся оценки с помощью МНК.

2. Методы линеаризации нелинейных моделей.

3. Метод Ньютона-Гаусса.

Продолжаем рассмотрение распространения изученного метода оценки и анализа регрессионных моделей. Мы познакомились с методами использования качественных факторов в регрессионных моделях, теперь познакомимся с возможностями построения некоторых типов нелинейных моделей.

Во многих практических случаях моделирование экономических зависимостей с помощью линейных уравнений дает вполне удовлетворительные результаты и может использоваться для анализа и прогнозирования поведения экономических объектов. Однако в силу многообразия и сложности экономических процессов ограничиться рассмотрением только линейных моделей невозможно. Многие экономические зависимости не являются линейными по своей сути, и поэтому их моделирование возможно лишь на основе нелинейных уравнений регрессии.

Например, зависимость объема выпуска продукции и основными факторами производства – трудом и капиталом (производственная функция Коба-Дугласа), зависимость спроса на товары и услуги от цены и располагаемого дохода являются по своей сути нелинейными.

Выбор вида зависимости осуществляется на основании содержательного анализа исследуемого явления, а также по результатам анализа характера взаимосвязи переменных, входящих в модель. Основной прием, который используется для построения нелинейных регрессионных моделей – линеаризация, который заключается в искусственном преобразовании исходной спецификации модели к линейному виду.

Различают два вида нелинейных моделей: нелинейные модели по переменным и нелинейные модели по параметрам. Рассмотренная модель множественной линейной модели является линейной одновременно по переменным и по параметрам.

Рассмотрим следующие типы нелинейных моделей, которые удается линеаризовать и затем оценить с помощью МНК.

1. Обобщенная нелинейная по аргументам модель:

(8.1)

2. Степенные функции:

(8.2)

3. Показательная функция (экспоненциальная):

(8.3)

4. Показательно-степенная:

(8.4)

Рассмотрим методы построения перечисленных типов моделей.

Начнем с обобщенной нелинейной по аргументам модели (8.1).

Если функции f_j зависят только от вектора экзогенных переменных и не зависят от неизвестных параметров, то для линеаризации модели (8.1) достаточно произвести замену переменных:

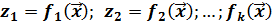(8.5)

Подставляя (8.5) в уравнение (8.1), получим спецификацию линейной модели множественной регрессии:

(8.6)

Получив спецификацию модели (8.1) в виде (8.6), следующим шагом необходимо по известным значениям наблюдений за вектором 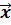и виду функций f_j подготовить выборку значений вектора переменных . Далее оценка и анализ модели (8.6) проводится по изученной выше последовательности.

Функцией (8.1) часто пользуются для описания поведения объектов с помощью степенных рядов, полиномоидальные модели. В качестве аргумента в полиномоидальных моделях часто выступает время. В этом случае спецификация модели выглядит так:

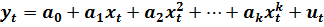(8.7)

В качестве примера рассмотрим модель динамики роста производства в Финляндии. Диаграмма рассеяния свидетельствует о нелинейности зависимости объема производства от времени рис. 8.1. На рисунке приведена диаграмма рассеяния результатов наблюдения за выпуском продукции по годам, в период с 1961 по 1996 гг. По виду расположения точек на диаграмме рассеяния сделано предположение о возможности описания процесса с помощью параболы второй степени.

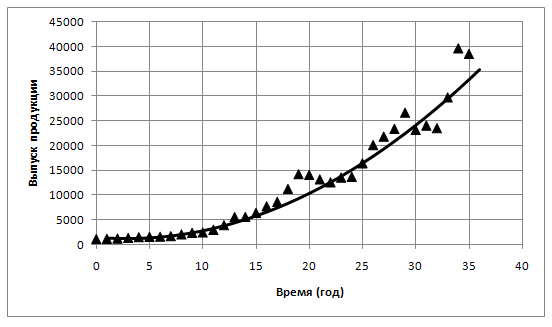
Рис. 8.1. Диаграмма рассеяния и график зависимости объема выпуска продукции с помощью параболы второй степени.

Спецификация такой модели имеет вид:

Оценка модели получилась следующей:

Как видно из рис. 8.1. парабола второй степени достаточно хорошо описывает характер зависимости.

Параболические модели широко применяются

- при моделировании средних и предельных издержек в зависимости от объема выпуска продукции

- при моделировании зависимости прибыли предприятия от расходов на рекламу

Кубические модели

– при моделировании общих издержек в зависимости от объема выпуска продукции

Вид функций модели (8.1.) может быть любой.

На практике часто используются модели гиперболические и полулогарифмические.

Модели гиперболического типа нашли широкое применение при моделировании

- зависимости спроса от цен;

- зависимости спроса от дохода (кривые Эйнгеля);

- спрос на предметы роскоши от дохода (функции Торнквиста);

- уровня относительного изменения заработной платы в зависимости от относительного изменения уровня безработицы (кривая Филипса).

Модель гиперболического типа имеет вид (для простоты рассмотрим модель парной регрессии):

(8.8)

Сделав замену переменной , получим спецификацию линейной модели парной регрессии с экзогенной переменной z.

В таб. 8.1. приведены исходные данные для построения модели Эйнгеля, а на рис. 8.2. диаграмма рассеяния и графики линейной и гиперболической моделей, построенных по данным таб. 8.1.

Таблица 8.1

Оцененная линейная и гиперболическая модели имеют вид:

Отметим, что кроме того, что гиперболическая модель значительно точнее описывает реальные данные, меняется и интерпретация параметров модели. В линейной модели параметр 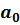это минимально необходимый объем потребления (при ), а параметр 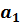- предельное потребление по доходу. В гиперболической модели параметр 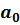максимальное возможное потребление при неограниченном доходе, а параметр 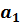теряет экономический смысл.

Рис. 8.2. Диаграмма рассеяния, линейная и гиперболическая модели.

Полулогарифмические модели имеют вид:

Такие модели используются в случаях, когда необходимо определить темп роста или темп прироста каких-либо экономических показателей. Например, при анализе банковского вклада по его первоначальному значению и процентной ставки, при исследовании зависимости прироста объема выпуска от относительного увеличения затрат ресурсов, бюджетного дефицита от темпа роста ВНП, темпа роста инфляции от объема денежной массы в обращении и т.п.

Полулогарифмическая модель:

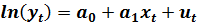(8.9)

Легко линеаризуется с помощью замены переменных . Коэффициент 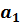в модели (8.9) имеет смысл темпа прироста переменной y по переменной x, т.е. характеризует отношение относительного изменения y к абсолютному изменению x. Действительно, продифференцировав уравнение (8.9) по x, получим:

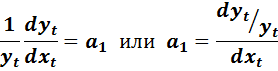
Умножив 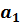на 100, получим процентное изменение переменной y (темп прироста).

Замечание. Недостатком метода замены переменных заключается в том, что вектор оценок неизвестных параметров модели находится не из условия минимума суммы квадратов отклонений исходных переменных, а из условия минимизации суммы квадратов отклонений преобразованных переменных. В связи с этим может понадобиться уточнение полученных оценок.

Дата добавления: 2015-10-29