Виды математических моделей ИСО

Основные понятия и особенности исследования операций

Термин "операционные исследования", по-видимому, впервые применил в 1938 г. А.Раув, руководитель научной группы в Бодси (Англия), отнеся его к работам по оценке эффективности операций, проводимых военно-воздушными силами. Однако сегодня больше используют американский термин "исследование операций", имеющий тот же смысл.

Возникнув в недрах военных ведомств, новая наука, развиваясь, находит применение в самых разных областях человеческой деятельности, в том числе в бизнесе.

В настоящее время исследование операций можно рассматривать как одну из важнейших дисциплин, связанных с принятием решений, или как составную часть системного анализа. Суть исследования операций остается неизменной: всесторонний анализ операции, оценка последствий возможных решений, поиск наиболее эффективных вариантов достижения цели. Приведем одно краткое определение, отражающее его главное предназначение:

Исследование операций (ИСО)- это наука о количественном обосновании оптимальных решений.

При этом под оптимальным понимается решение, наилучшее в определенном смысле. Нельзя говорить об оптимальном решении вообще, корректное применение этого понятия требует конкретизации его смысла и условий, в которых принимается решение.

В то же время " операция "- широкое понятие: это есть совокупность действий или мероприятий, направленных на достижение определенной цели. В ИСО описание операции включает следующее.

1. Цель операции, то есть то, ради чего проводится операция.

2. Оперирующая сторона - лицо или группа лиц, преследующих поставленную цель. В сложных операциях оперирующая сторона состоит из лица, принимающего решение (ЛПР), и аналитиков - специалистов по исследованию операций. Физически ЛПР - это одно лицо или группа лиц, наделенных правом принимать решения и несущих за них ответственность. Подготовка решений ложится на аналитиков. Разница между первыми и вторыми не только в знаниях методологии и методов ИСО, но и в информированности об операции. Причины этого кроются в сложности извлечения и представления информации, которой владеет ЛПР, или в нежелании ЛПР раскрывать все карты. В простых случаях ЛПР и аналитик могут быть в одном лице.

3. Активные средства - это, как правило, ресурсы, используемые для достижения цели.

4. Способы действий, поведения или использования активных средств. Их называют решениями, альтернативами или стратегиями в зависимости от типа операции.

5. Результаты или исходы операции.

6. Тип связи между решениями (стратегиями) и исходами операции. Он зависит от условий, в которых протекает операция.

Говоря об ИСО как о самостоятельном направлении, обычно отмечают его три основные особенности: системный подход, комплексный коллектив исследователей, применение научных методов.

Под системным подходом понимается комплексная методология исследования сложных систем или проблем. В этой методологии определяющим является подход к любой части системы (проблемы) с позиции системы в целом, превалирование цели системы над целями ее подсистем. Другое важнейшее требование системного подхода состоит в том, что необходимо стремиться выявить все существенные факторы и взаимосвязи, влияющие на достижение цели системы. Для этого приходится расширять первоначальный объект исследования, искать скрытые от первого взгляда связи между факторами и частями системы.

Вторая особенность ИСО обусловлена необходимостью изучения и анализа проблемы с разных точек зрения, стремлением выйти за рамки стереотипов. Именно поэтому с момента возникновения исследования операций группы исследователей состояли из специалистов разного профиля (военных, математиков, физиков, психологов и др.), объединенных единой методологией. Такое комплексное исследование позволяет расширять множество альтернатив и находить действительно наилучшее решение.

Применение научных методов присуще любой науке, но в ИСО они имеют свою специфику, которая обусловлена задачей исследования и количественным характером результатов. Чтобы яснее представить эту особенность ИСО, рассмотрим, как проводится операционное исследование.

Этапы операционного исследования и их содержание

Не существует строгой регламентации хода и содержания операционного исследования, но в любом выполненном проекте можно выделить характерные для ИСО этапы разработки.

1. Постановка задачи. Она включает содержательное описание задачи: объект и цель исследования, внутренние и внешние условия, ресурсы, значения параметров или их оценки, возможные способы действий и возможные результаты, другую имеющуюся информацию. Эту работу выполняют совместно ЛПР и аналитик. После тщательного анализа первоначальной постановки аналитик уточняет с ЛПР содержание задачи по всем аспектам и особо согласовывает показатель, который предлагается в качестве критерия оптимальности.

2. Построение математической модели. Характер задач исследования операций таков, что их решение не может проводиться путем натурного эксперимента или физического моделирования. Например, выбор места и мощности нового производства, определение оптимального плана выпуска продукции, формирование портфеля заказов немыслимо производить путем реализации и сравнения различных вариантов. Такая ситуация в науке не нова: так в астрономии нельзя манипулировать небесными телами, но предсказывать положение планет солнечной системы возможно благодаря использованию математической модели. Модели, и в частности математические, широко применяются в различных областях. Математические модели исследования операций отличаются своей направленностью, которая отражается в структуре модели. Математическая модель в ИСО включает:

зависимость критерия от управляемых и неуправляемых переменных;

уравнения, отражающие связи между переменными, например, уравнения на основе материально-энергетических балансов;

ограничения, обусловленные реальными условиями и требованиями к показателям и переменным (неотрицательность, целочисленность, комплектность, допустимые и/или директивные значения и т.п.). В конкретных задачах могут отсутствовать отдельные составляющие модели полностью или частично за исключением критериальной функции, которая должна быть в модели обязательно.

3. Проверка адекватности модели. Математическая модель представляет собой формализованную гипотезу исследователя о реальных взаимосвязях и поведении системы. Поэтому прежде чем использовать модель для прогнозирования последствий и выбора решений, необходимо убедиться в ее адекватности системе или операции с точки зрения поставленной цели исследования. Для "прозрачных" моделей может быть достаточной качественная проверка, в сложных моделях необходим количественный анализ. В последнем случае для моделирования поведения на модели используются численные методы (иногда это называют прямой задачей: по задаваемым входам нужно определить выходы). Для осуществляемых ранее операций проверка адекватности может производиться по ретроспективным данным (при отсутствии качественных изменений в операции). В других случаях проверка проводится путем наблюдения за реакцией модели и системы на одинаковые решения. При обнаружении неадекватности модель корректируется: при качественном совпадении повысить количественную адекватность можно путем уточнения коэффициентов модели, при более серьезных расхождениях может потребоваться изменение и/или добавление ограничений и уравнений или даже построение другого вида модели. Следует заметить, что такая проверка невозможна для вновь разрабатываемых операций, и тогда приходится довольствоваться качественным тестированием модели.

4. Поиск оптимального решения на модели. Это центральный этап операционного исследования (с математической точки зрения - обратная задача). Он заключается в определении решения, оптимального в смысле принятого критерия. Для отыскания оптимального решения на математической модели применяются методы оптимизации, главным образом методы математического программирования.

5. Анализ оптимального решения. Сюда входит анализ чувствительности полученного решения, параметрический и вариантный анализ, выявление альтернативных оптимальных решений и др. Анализ чувствительности критерия к отклонению переменных от их оптимальных значений позволяет определить разумные требования к точности реализации оптимального решения. Результаты параметрического и вариантного анализа показывают, каким будет оптимальное решение при изменении коэффициентов модели, состава ограничений или при изменении критерия. При этом может устанавливаться значимость отдельных элементов модели, то есть их влияние на оптимальное значение критерия. В случае неединственности оптимального решения появляется дополнительная возможность выбора по показателю, который не представлен в критерии. Важное место в анализе решения отводится интерпретации полученных результатов в терминах предметной области Л ПР.

6. Внедрение результатов исследования. Здесь главное требование состоит в необходимости непосредственного участия разработчиков на всех стадиях реализации предлагаемых решений.

Таким образом, применение научных методов в ИСО отличается всесторонним количественным исследованием, основанным на математической модели и ставящим своей целью определение оптимального решения в интересах ЛПР.

Критерий оптимальности

Поставленная в операции цель может быть достигнута по-разному и в разной степени в зависимости от принимаемых решений. Критерий есть тот показатель, который характеризует (оценивает) эффективность решений с точки зрения достижения цели, а следовательно, позволяет выбрать среди них наилучшее. В ИСО применяют равнозначные термины: критерий оптимальности, критерий эффективности, целевая функция. Последний термин подчеркивает неразрывную связь критерия с целью. Таким образом, решение может быть оптимальным только в смысле конкретного критерия в пределах адекватности используемой модели.

В исследовании операций к критерию предъявляются определенные требования. Наиболее важные из них следующие.

1. Критерий должен быть количественной и неслучайной величиной.

2. Критерий должен правильно и полно отражать поставленную цель. Его можно рассматривать как количественную модель качественной цели.

3. Критерий должен иметь простой и понятный ЛПР физический смысл.

4. Критерий должен быть чувствителен к управляемым (искомым) переменным.

При исследовании действующих систем к критерию могут предъявляться дополнительные требования, такие как измеримость, статистическая однозначность, статистическая эффективность и др.

Множество показателей, которые в ИСО используются в качестве критериев, можно условно разделить на ряд групп: социальные (среднедушевой доход, обеспеченность жильем и т.п.), экономические (прибыль, рентабельность, себестоимость и др.), технико-экономические (производительность, урожайность и др.), технико-технологические (прочность, чистота материала, другие физические или химические показатели), прочие. Они приведены в порядке убывания глобальности применения: первые применяются в системах более высокого уровня (страна, регион, предприятие), последние - в основном на уровне процесса, объекта.

Однако во многих случаях не удается полностью отразить поставленную цель одним критерием и тем более это невозможно, когда в операции преследуется более одной цели. Например, цели типа повышение уровня жизни, улучшение экологической обстановки и т.п. нельзя "покрыть" одним критерием. В таких ситуациях вводится несколько показателей, характеризующих достижение цели. Как правило, оптимальные решения, получаемые по разным показателям-критериям, не совпадают, что создает неопределенность в выборе окончательного решения. Задачи, в которых приходится определять наилучшее решение по нескольким критериям, называются многокритериальными или задачами векторной оптимизации. Они составляют особый и более сложный класс задач исследования операций.

Виды математических моделей ИСО

Рассмотрим виды математических моделей только в одном аспекте, который обусловливает принципиальные различия математических моделей и методов отыскания на них оптимальных решений.

Вид модели определяется типом связи между решениями (альтернативами, стратегиями) и результатами, который в свою очередь зависит от условий, в которых протекает операция и приходится принимать решения.

1. Решения принимаются в условиях определенности. Это значит, что каждому решению можно поставить в соответствие (пусть даже путем сложных расчетов) определенный результат, то есть имеет место детерминированный тип связи. Модели, описывающие такие ситуации, называются детерминированными. Этот тип модели на практике применяется наиболее широко, так как он "удобен в работе". По этой причине такие модели часто используют в качестве первого приближения и в условиях, отличающихся от ситуации определенности.

2. Решения принимаются в условиях риска. Между решениями и результатами имеет место стохастическая связь: определенному решению может соответствовать более одного результата, вероятности появления которых известны. Адекватным отображением таких условий являются вероятностные (стохастические)модели. Если под результатом имеется в виду значение критерия, то исходная постановка задачи (и модель) некорректна: нельзя максимизировать или минимизировать случайную величину. В этом случае в качестве критерия следует выбирать не исходный показатель, а одну из его вероятностных характеристик, например, математическое ожидание или дисперсию. Неоднозначность обусловлена наличием случайных факторов. Но осреднение случайных аргументов и осреднение результатов, на которые первые влияют, далеко не всегда одно и то же. Это объясняется тем, что в общем случае не выполняется равенство

М [ f (x ₁, x ₂,..., x_n)] = f [ M (x ₁), M (x ₂),..., M (x_n)], (1.1)

где x_j - случайные величины, М -знак математического ожидания.

Рассмотрим пример такой ситуации. Пусть фирма "Апельсин" постоянно занимается продажей фруктов. Для простоты будем считать, что поставка и продажа фруктов осуществляется целыми контейнерами, а единицей времени является неделя. Спрос на фрукты С колеблется случайным образом, но вероятность спроса в случайно взятую неделю Р (С)известна. При заключении договора с поставщиком на очередной период фирма должна определить наиболее выгодное для нее количество контейнеров, которое будет поставляться еженедельно, если известны прибыль от реализации одного контейнера d и убыток b при его невостребовании. Так как спрос случаен, то и результат - доход за неделю D для фиксированного числа заказываемых контейнеров п будет случайной величиной: в случае, когда спрос превысит предложение, то есть при С > п,

D = dn; (1.2)

если же предложение окажется выше спроса (С < п),доход

D = dn -(n - C) b. (1.3)

Таким образом, доход D является функцией управляемой величины п и случайного фактора С. Очевидно, что максимизация такого показателя бессмысленна. В качестве критерия оптимальности разумно взять математическое ожидание дохода за неделю, так как его максимизация обеспечит максимум дохода за весь период. Поскольку вероятность появления случаев (1.2) и (1.3) определяется P (С), то модель задачи будет иметь вид

M [ D ] = = + max, (1.4)

n >0,int, (1.5)

где int означает "целое". При составлении этой модели в явном виде учитывалась стохастичность ситуации и, следовательно, принимаемые по ней решения в такой же степени учитывают фактор случайности. Упрощенное представление операции может базироваться на аппроксимации реальной ситуации детерминированной. В этом случае спрос рассматривается как неслучайная величина, равная его математическому ожиданию . При этом доход

D =

также неслучаен. На такой модели оптимальное решение, максимизирующее D, определяется просто: п ⁰ = С.

Чтобы показать отличие результатов при использовании упрощенной модели и модели (1.4), произведем расчет для исходных данных d =30, b =5и вероятности спроса:

C
P (C)		0,1	0,25	0,3	0,25	0,1

Вычисляем средний спрос: С = =3. Тогда по упрощенной модели получим: п ⁰ = 3, D =90. Такой доход имел бы место при детерминированном и неизменяемом уровне спроса. Но при случайном спросе величина D =90 будет достигаться только в те недели, когда спрос окажется не меньше 3, а в другие недели доход будет ниже и, следовательно, средний доход за весь период станет меньше 90. Чтобы показать это и одновременно определить оптимальное число контейнеров при случайном спросе, вычислим значения среднего дохода по модели (1.4) при всех возможных п:

n
		56,5	74,25	81,5

По результатам вычислений видно, что решение n ⁰=3, полученное на детерминированной модели, не обеспечивает максимального среднего дохода. Кроме того, видно, что в условиях случайного спроса оптимальным является решение п =4, при котором средний доход составляет 81.5 против 74.25 при n ⁰=3. Это пример операции, для которой не выполняется равенство (1.1), хотя случайный фактор имеет симметричное распределение. Судя по разнице результатов на двух моделях, в данной операции стохастичность оказывает значимое влияние и поэтому ее нельзя не учитывать.

Однако наличие случайных факторов не всегда влечет за собой неоднозначность результатов. Возможны случаи, когда элементарные составляющие процесса или системы ведут себя случайно, а результаты системы в целом не случайны. Характерным примером такой системы является идеальный газ, поведение которого подчиняется детерминированному закону Бойля-Мариотта. Неслучайное поведение на макроуровне при наличии элементов случайности на микроуровне называют стохастическим детерминизмом.

3. Решения принимаются в условиях неопределенности. Это ситуация, противоположная первой рассмотренной. Природа неопределенности может быть различной, но в общем случае она проявляется в том, что определенному решению соответствует более одного результата, а вероятностные характеристики результатов неизвестны. Математические модели, описывающие неопределенный тип связи, разнообразны и не имеют единого названия. В частности, к этому классу относятся матричные модели, модели типа "игра", "аукционный торг", нечеткие модели.

Во многих случаях ситуацию неопределенности можно представить (или аппроксимировать) матрицей вида

Альтер-нативы	Состояние среды
Q 1	Q 2	…	Qn
A 1	u 11	u 12	…	u 1 n
A 2	u 21	u 22	…	u 2 n
…	…	…	…
Am	um 1	um 2	…	umn

где u_ij - результат (исход) выбора альтернативы А_i при условии, что среда окажется в состоянии Q_j; u_ij может иметь смысл прибыли, дохода, выигрыша или затрат, проигрыша, убытков и т.п.).

Прежде чем выбирать решение на этой модели, нужно определиться с принципом оптимальности, на основе которого будут сравниваться альтернативы, так как только одно желание ЛПР получить наилучший результат не дает такой основы. Принцип оптимальности зависит от точки зрения на ситуацию ЛПР, его отношения к риску, от предположений относительно поведения среды. Наиболее характерной гипотезой поведения среды является представление, что среда ведет себя наихудшим образом ("как назло"). Это самый пессимистический взгляд на ситуацию, свойственный ЛПР, не склонному к риску. В этом случае выбор решения основывается на принципе гарантированного результата (иногда его называют критерием Вальда). Он состоит в том, что эффективность каждой альтернативы оценивается наихудшим из исходов, возможных при выборе данной альтернативы. Такой результат гарантируется, то есть будет не хуже, при любом фактическом состоянии среды. Теперь очевидно, что наилучшим решением в смысле принятого принципа оптимальности будет выбор той альтернативы, которая имеет наилучший гарантированный результат. Так, если u_ij имеет смысл прибыли, то оценкой i -й альтернативы является 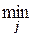u_ij, а оптимальной будет альтернатива, максимизирующая эту величину, то есть A _i,на которой достигается 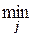u_ij. Применительно к этой ситуации принцип гарантированного результата называют принципом максимина,а оптимальную альтернативу - максиминной. В условиях неопределенности только этот принцип имеет объективное обоснование и дает абсолютно надежную оценку.

Другой подход, называемый также критерием Сэвиджа, использует аналогичный прием, но по отношению к преобразованной матрице - матрице риска (сожалений) [ r_ij ], где r_ij = u_ij - u_ij, то есть риск - это разность между максимально возможным выигрышем при j -м состоянии среды и выигрышем при выборе i -й альтернативы в условиях незнания о фактическом состоянии среды. Так как цель состоит в уменьшении риска, то, используя принцип минимакса (гарантированного риска), определим как оптимальную ту альтернативу, на которой достигается 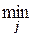u_ij, тогда риск не превысит этой величины ни при каком состоянии среды.

Гибкий учет отношения ЛПР к риску возможен с помощью критерия Гурвица. Если исходы имеют смысл дохода, то оптимальная альтернатива определяется из условия

{ g u_ij +(1- g) 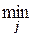u_ij },

где g = [0, 1] - коэффициент риска. При ориентации на самое худшее g = 0,что соответствует критерию Вальда, а для крайнего оптимиста g = 1. Промежуточные значения g отражают разный уровень риска ЛПР.

Возможны и другие подходы к выбору оптимальных решений в условиях неопределенности, но все они, как и последние два, не гарантируют достижение расчетных результатов.

Как следует из вышерассмотренного, выбор вида модели требует от исследователя интуиции и опыта наряду с глубокими знаниями моделируемой области. Следует особо отметить, что построение модели основывается на представлениях аналитика, которые могут не соответствовать реальным связям в большей или меньшей степени. При этом большое значение имеют оценка влияния случайных факторов, факторов неопределенности, уровень агрегирования, допустимая сложность модели. Так, нередко возникает дилемма: построить высокоточную, но очень сложную модель, на которой можно будет получить только приближенное к оптимальному решение, либо поступиться точностью моделирования и иметь возможность применять на модели точные методы оптимизации. Какое решение окажется ближе к истинному оптимальному, заранее сказать невозможно. К сожалению, не существует готовых рецептов построения математических моделей. Это один из этапов операционного исследования, который, следуя Саати, можно отнести к области искусства.

Дата добавления: 2015-10-29