Степенная модель.

(8.10)

Степенные модели достаточно широко используются в экономике. К классу степенных функций относятся, в частности, модели спроса и предложения (кривые Эйнгеля), производственные функции, кривые освоения для характеристики связи между трудоемкостью продукции и масштабами производства в период освоения и выпуска нового вида продукции, а также зависимость валового национального дохода от уровня занятости.

Метод линеаризации степенных моделей заключается в логарифмировании обеих частей уравнения (8.10):

(8.11)

Далее делается замена переменных:

(8.12)

Подставив переменные (8.12) в (8.11) получится знакомое уравнение множественной линейной регрессии относительно новых переменных:

(8.13)

Для спецификации (8.13) формируется выборка наблюдений в соответствии с (8.12) и производится оценка и анализ полученной модели. Чтобы получить модель в исходном виде достаточно произвести обратную замену.

Замечание. Остается открытым вопрос, по какому основанию логарифмировать уравнение (8.10). Вообще говоря, по любому. На практике используют либо натуральное основание, либо десятичное.

Интерес представляет экономическая интерпретация параметров степенной модели. Рассмотрим для примера производственную функцию Коба-Дугласа:

(8.14)

Вычислим производную функции (8.14) по фактору производства K.

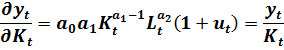
Откуда следует, что:

(8.15)

Выражение (8.15) представляет собой определение коэффициента эластичности переменной y по переменной x.

Таким образом, получили, что показатели степени при переменных в мультипликативной степенной модели являются соответствующими коэффициентами эластичности. Это важное свойство степенных моделей.

Показательная (экспоненциальная) функция:

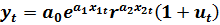(8.16)

Основанием степени модели (8.16) может быть любым. В случае, когда в качестве основания степени используется константа e, модель (8.16) называют экспоненциальной.

Показательные модели характеризуются постоянным темпом относительного прироста эндогенной переменной. Действительно, если пренебречь влиянием случайного возмущения, то в результате дифференцирования (8.16) по каждому из регрессоров получим:

Тогда относительный прирост эндогенной переменной равен:

(8.17)

Таким образом, параметры при регрессорах в показательных моделях имеют смысл коэффициентов относительного прироста.

Линеаризация модели (8.16) производится с помощью логарифмирования:

С помощью несложной замены переменных полученное уравнение приводится к линейному виду:

(8.18)

Для вычисления оценок исходных параметров достаточно использовать следующие зависимости:

(8.19)

Здесь s основание логарифма. На практике показательные модели с разными основаниями встречаются редко. В случае одинакового основания (e или «10») вычисления несколько упрощаются.

Практический интерес представляет логистическая функция, которая является частным случаем показательной модели.

(8.20)

График функции (8.20) имеет две горизонтальные асимптоты и и точку перегиба . Линеаризация модели (8.20) производится с помощью перехода к переменным

.

Логистические функции используются для описания поведения экономических показателей, имеющих уровни «насыщения». Например, для описания зависимости спроса на товар от дохода, развитие производства нового товара от роста численности населения и т.п.

Показательно-степенные модели представляют собой произведение показательной и степенной модели. Простейший пример такой модели можно представить в виде:

(8.21)

Линеаризация модели (8.21) также производится с помощью логарифмирования и последующей замены переменных:

(8.22)

С помощью новых переменных:

уравнение (8.22) преобразуется к линейному виду.

Замечание. Линеаризация путем логарифмирования и последующей замены переменных имеет тот же недостаток, который заключается в том, что вектор оценок неизвестных параметров модели находится не из условия минимума суммы квадратов отклонений исходных переменных, а из условия минимизации суммы квадратов отклонений преобразованных переменных. В связи с этим может понадобиться уточнение полученных оценок.

Алгоритм оценивания нелинейных моделей сводится к следующему. Линеаризованная модель оценивается и исследуется на качество спецификации, гомоскедастичность и автокорреляцию. После чего, осуществляется обратный переход к исходной модели. Для этого необходимо вычислить оценку параметров, оценку их ошибок и ошибку прогнозирования. Значения оценок параметров при регрессорах и их ошибок не изменяются (см. (8.22) и (8.11)). Значение оценки параметра , и ошибка прогнозирования вычисляются следующим образом:

где: - оценка ошибки прогнозирования по линеаризованной модели.

Рассмотрим в заключение вопрос, как оценить нелинейную по параметрам модель, поведенческая функция которой не поддается линеаризации.

В общем виде спецификацию такой модели можно записать в следующем виде:

(8.23)

где: – вектор параметров модели.

В этом случае не удается получить систему нормальных уравнений для вычисления оценок параметров модели в линейном виде и, следовательно, процедура нахождения оценок параметров, сформулированная в теореме Гаусса-Маркова, не применима. Задача оценки параметров модели (8.23) может быть решена, в частности, следующим образом (метод Ньютона-Гаусса).

Шаг 1. Записывается выражение для квадрата ошибок:

(8.24)

и формулируется задача нелинейного программирования:

(8.25)Задача (8.25) может содержать ряд ограничений относительно параметров модели. Задача (8.25) может быть решена относительно неизвестных параметров одним из численных методов поиска экстремума функции, в частности, методом сопряженных градиентов (направлений), который запрограммирован в функции «Поиск решения» табличного процессора EXCEL. В результате будут получены приближенные значения оценок параметров модели, при которых справедлив метод наименьших квадратов.

Шаг 2. Остается оценить ошибки полученных на шаге 1 оценок параметров. Предполагается, что функция (8.23) является гладкой в некоторой окрестности точки полученных значений оценок параметров: . Тогда значение функции (8.23) в точке можно представить в виде:

(8.26)

Здесь неизвестные поправки к известным значениям компонент вектора .

С помощью замены переменных:

Линейная модель (8.23) трансформируется в линейную модель:

(8.27)

В модели (8.27) неизвестными параметрами являются .

Оценив модель (8.27) каким-либо подходящим методом, можно рассчитать оценки и ошибки исходных параметров:

В результате удается вычислить, как оценки параметров, так и их ошибки модели (8.23).

Дата добавления: 2015-10-29