Множественная линейная регрессионная модель. Оценивание параметров множественной регрессии методом наименьших квадратов

Множественная линейная регрессия позволяет построить и проверить модель линейной связи между одной зависимой (эндогенной) и несколькими независимыми (экзогенными) переменными: y = f(x₁,...,x_р), где у - зависимая переменная (результативный признак); х₁,...,х_р - независимые переменные (факторы).

Для построения уравнения множественной регрессии чаще используются следующие функции:

ü Линейная – y=a+b₁x₁+b₂x₂+…+b_px_p+ε

ü Степенная -

ü Экспонента -

ü Гипербола -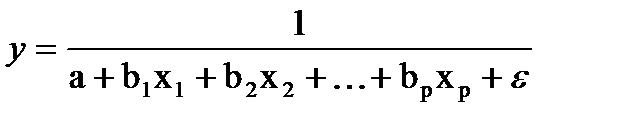

Можно использовать и другие функции, приводимые к линейному виду

Спецификация модели включает в себя два круга вопросов: отбор факторов и выбор вида уравнения регрессии. Требования к факторам.

1. Они должны быть количественно измеримы.

2.Факторы не должны быть коррелированы между собой и тем более находиться в точной функциональной зависимости.

Независимая переменная Y характеризует состояние или поведение экономического объекта. Набор переменных X ₁,…, X_k, характеризуют этот экономический объект качественно или количественно. Предполагаем, что переменные X оказывают влияние на переменную Y, т. е. реализации переменной Y выступают в виде функции, значения которой определяются. правда, с некоторой погрешностью, значениями объясняющих переменных, выступающих в роли аргументов этой функции, т. е.

Y = f (X ₁,…, X_k) + e,

где e - случайная компонента

МЛРМ –

Пример:

где Q^D - объем спроса на масло,

Х - доход,

P - цена на масло,

PM - цена на мягкое масло.

Здесь нам неизвестны коэффициенты b и параметры распределения e.

Для их оценки имеется выборка из N наблюдений над переменными Y и X ₁,…, X_k.

Для каждого наблюдения должно выполнятся следующее равенство:

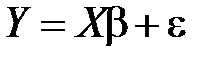Матричная форма записи МЛРМ

Где

Метод наименьших квадратов

Среди всех возможных гиперплоскостей выбираем ту, для которой сумма квадратов остатков минимальна

Будем минимизировать

Минимизация

или

Система нормальных уравнений

Вывод формулы для нахождения коэффициентов в матричном виде

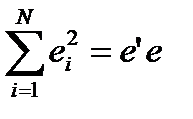
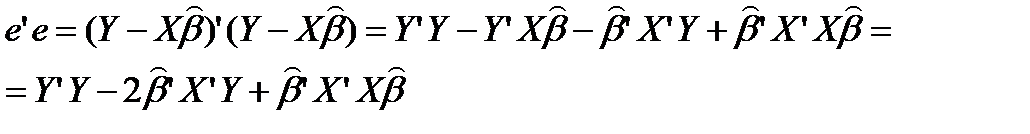Вывод формулы для нахождения коэффициентов в матричном виде

итог

- МНК оценки коэффициентов МЛРМ

Дата добавления: 2015-10-23