Определение границ доверительного интервала

1) Находим оценки параметров спецификации (коэффициенты регрессии а^0, а^1, а^2, оценки среднеквадратичного отклонения коэффициентов регрессии S_a0, S_a1, S_a2 и т.д.):

2) Далее, выбираем строку и обозначаем ее прогнозом. Настоящее значение функции обозначим Yp.

3) Следующим шагом необходимо рассчитать прогнозное значение Y^p, используя полученные оценки коэффициентов регрессии (см. рисунок).

В большинстве случаев налицо явное несовпадение результата и прогноза. Но ожидать точное совпадение прогноза и результата по меньшей мере наивно. Во-первых, Y^p - величина случайная, т.к. все три оценки коэффициентов a^0, a^1, a^2 вычислялись через значения случайной величины Y. Во-вторых, значение Yp содержит в себе неизвестное значение случайной составляющей ε_р. Все, что мы можем предпринять в этой ситуации, это проверить, попадают ли оба значения в доверительный интервал и делать заключение по этому факту.

Величина доверительного интервала зависит от дисперсии прогноза, которая складывается из дисперсии εt - случайной составляющей эконометрической модели и дисперсии случайной величины оценки регрессии (уравнение регрессии), значения коэффициентов которой вычислены с помощью функции ЛИНЕЙН (см. рисунок).

Однако оценки коэффициентов a^0, a^1, a^2 зависимы и для оценки их влияния на точность прогноза мало знать только их дисперсии, но нужно учесть и их взаимную зависимость, т.е. ковариацию, которая задается матрицей ковариаций.

Матрица ковариации регрессии оценивается по следующей формуле: Cov(A^) = S²_ε*(X^T*X)^-1, где A^ = (a^0, a^1, a^2)^T, оценки коэффициентов регрессии; S²_ε - дисперсия случайной составляющей ε.

4) Далее производим следующие вычисления:

1. (X^T*X)^-1.

2. 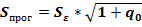, где .

5) Определим доверительный интервал для прогноза как (Y^p-tα*Sпрог, Y^p+tα*Sпрог), где tα-статистика Стьюдента, вычисляемая по формуле EXCEL СТЬЮДРАСПОБР.

Если оба значения (т.е. Yp и Y^p) попадают в указанный интервал, то модель признается адекватной и пригодной для целей прогнозирования.

Дата добавления: 2015-10-23