Модель парной регрессии. Границы доверительных интервалов

Наша задача – подобрать функцию так, чтобы она проходила на наименьшем расстоянии от всех точек сразу. Для этого необходимо минимизировать выражение 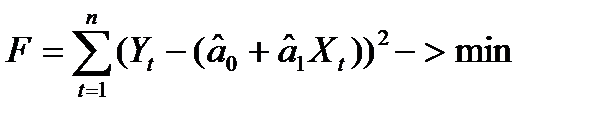Необходимые условия экстремума: 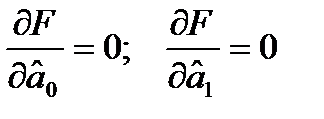Возьмем соответствующие производные и приравняем их к нулю: ; .

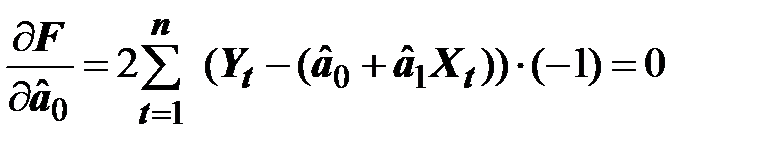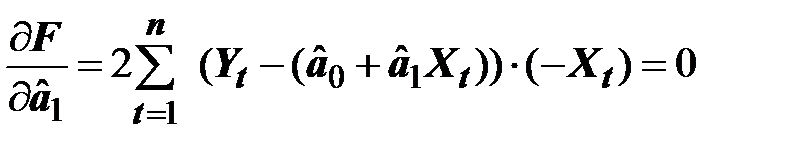Раскроем скобки и получим стандартную форму нормальных уравнений: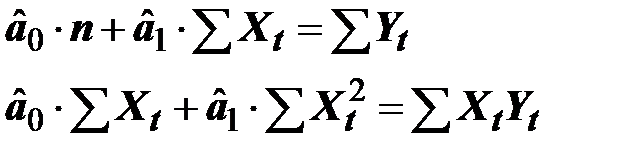

Решая систему уравнений относительно получаем их оценки:

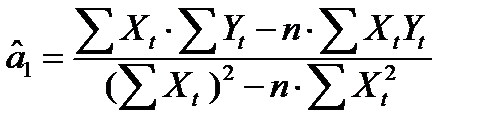
Из последнего уравнения получаем: 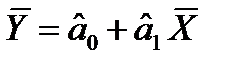. Это равенство указывает на то, что уравнение регрессии проходит через точку 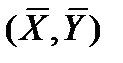. Обозначим 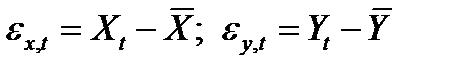. Подберем линейную функцию 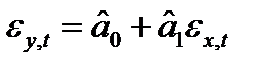минимизирующую функционал 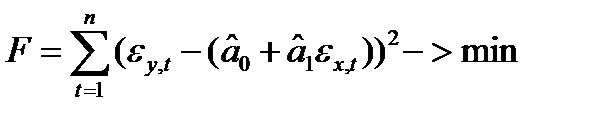. Это будет та же прямая, только в новых координатах, центр которых переместится в точку 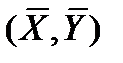. Так как 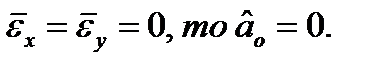и .

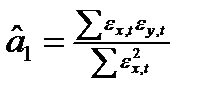Регрессионное уравнение имеет вид 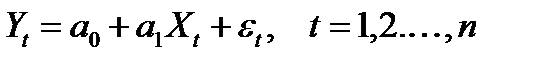, где Xt – случайная величина, не коррелированная с ε. εt – случайная величина. Yt – объясняемая (зависимая) переменная, Xt – объясняющая (независимая) переменная.Поскольку Yt является суммой случайной переменной Xt и случайной переменной ε t, то она сама является случайной величиной. Основные гипотезы относительно модели:

1. 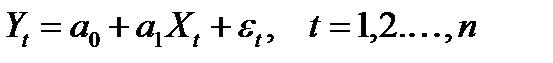- спецификация модели

2. Xt – случайная величина, не коррелированная с ε.

3. М(ε)=0

4. М(ε2)=σ2 = const - не зависит от t

5. M(εt, εs) = 0 при t ≠ s – некоррелированность значений случайной составляющей в различные моменты времени

Условия 3, 4, 5 называются условиями Гаусса-Маркова

Прогноз будущего (или пропущенного) значения эндогенной переменной определяется по уравнению регрессии. Найдем доверительный интервал, который с доверительной вероятностью Р = 1 – α будет накрывать значение зависимой переменной Y^{^}: .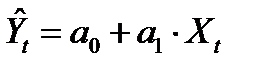

Доверительный интервал определяется разбросом случайной компоненты относительно уравнения регрессии. Причин этого разброса две:

· Оценки коэффициентов регрессии 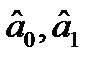являются величинами случайными и они сами по себе создают разброс относительно истинного уравнения регрессии.

· Случайная составляющая ε_t

Ошибка предсказания равна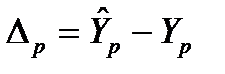

; ;

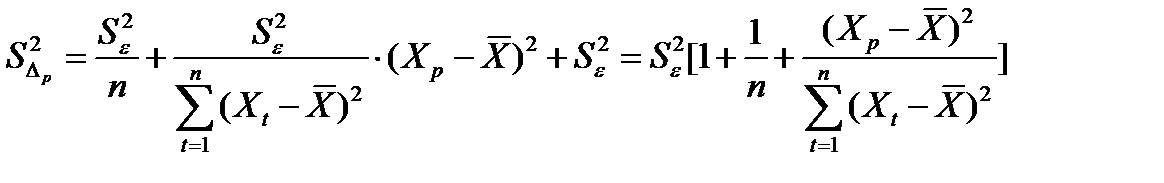
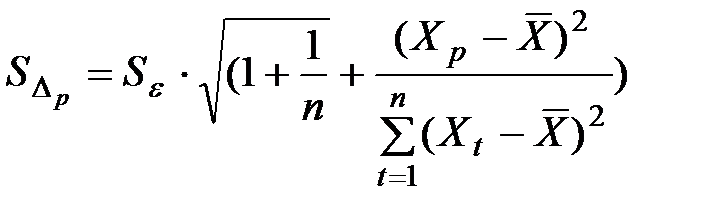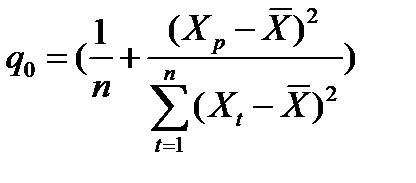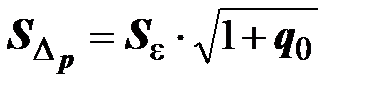
Тогда границы интервала будут задаваться так: (Y^ - tα*S∆p; Y^ + tα*S∆p), где tα - статистика Стьюдента.

Дата добавления: 2015-10-23