Гетероскедастичность случайной компоненты. Тесты на наличие гетероскедастичности

Одно из требований теоремы Гаусса-Маркова - дисперсия случайной компоненты

D( ) = = const,

т.е. предположение о постоянстве дисперсии случайной составляющей для всех наблюдений. Если это условие соблюдается, процесс e_t называется гомоскедастичным. Если это не так, то процесс называется гетероскедастичным. Для обнаружения гетероскедастичности используется метод Голдфельда-Квадта. При проведении проверки по этому тесту предполагается сначала, что стандартное отклонение σ является случайной составляющей пропорционально значению одной из независимых переменных: X_{1 t} или Х_2t.

Для того, чтобы осуществить проверку на гомоскедастичность, необходимо для начала сортировать имеющиеся данные по возрастанию одной из переменных X_{1 t} или Х_2t. Важное условие такой сортировки – неразрывность троек (X_1t,X_2t,Y_t), они могут перемещаться только вместе. В результате получаем новую таблицу, в верхней части которой сосредоточены меньшие значения Х_1t, а в нижней – б о льшие.

Далее делим получившийся массив данных на две (по возможности) равные части. Для каждой из частей определяем регрессию с помощью функции ЛИНЕЙН и выделяем значения ESS1 и ESS2.

Следующий шаг – вычисление статистик 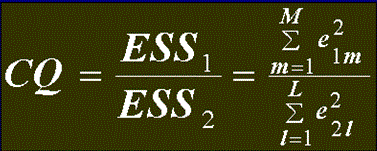(статистика Голдфельда-Квадта) и 1/GQ=ESS2/ESS1.

Статистика GQ является случайной величиной, распределенной по закону Фишера со степенями свободы числителя и степенями свободы знаменателя , где М – количество пар чисел в первой, а L – количество пар чисел во второй части выборки.

Далее находим значение F-статистики Фишера, используя уровень значимости α (обычно равен 0,05), а также количество степеней свободы первой и второй части списка; проверяем условия

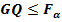
Если оба этих условия выполняются, то гипотеза о равенстве дисперсий в обеих половинах выборки принимается с вероятностью p=1-α. Если хотя бы одно из неравенств не выполняется, то гипотеза отвергается с той же вероятностью.

Дата добавления: 2015-10-23