Оценивание параметров модели взвешенным методом наименьших квадратов

Для практики полезно из теоремы Гаусса-Маркова выделить частный случай обобщенного метода наименьших квадратов, разработанный Гауссом в первой половине 19в. В этом частном случае, именуемом в эконометрике взвешенным методом наименьших квадратов (ВМНК), матрица является диагональной, но не скалярной, т.е.

Это означает, что предпосылка справедлива, а предпосылка нет, следовательно

(1)

Введем здесь обозначение: (2)

Определение Согласно предположенной Гауссом терминологии , определенная по правилу (2), называется весом случайной переменной . Понятие веса случайной переменной позволяет придать внятный смысл константе : это дисперсия такой случайной переменной, вес которой равен единице; иногда такую случайную переменную именуют (термин Гаусса) единицей веса.

С учетом (1) матрица в процедуре

оказывается диагональной:

из формулы упрощается:

В свою очередь свойство обобщенных наименьших квадратов, справедливое для оценки Эйткена , трансформируется в свойство взвешенных наименьших квадратов: = Отметим, что матрицу (3) называют матрицей весов, а обратную к ней матрицу Ω – матрицей обратных весов или весовых коэффициентов.

Модель Марковица

Модель основана на том, что показатели доходности различных ценных бумаг взаимосвязаны: с ростом доходности одних бумаг наблюдается одновременный рост по другим бумагам, третьи остаются без изменения, а по четвертым доходность, наоборот, снижается. Такая зависимость не является детерминированной, т.е. однозначно определенной, а есть стохастической и называется корреляцией.

Модель Марковица имеет следующие основные допущения:

— в качестве доходности ценной бумаги принимается математическое ожидание доходности;

— в качестве риска ценной бумаги принимается среднее квадратическое отклонение доходности;

— принимается, что данные прошлых периодов, используемые при расчете доходности и риска, в полной мере отражают будущие значения доходности;

— степень и характер взаимосвязи между ценными бумагами выражается коэффициентом линейной корреляции.

По модели Марковица доходность портфеля ценных бумаг — это средневзвешенная доходность бумаг, его составляющих, и она определяется формулой:

где N — количество ценных бумаг в портфеле; — процентная доля данной бумаги в портфеле; — доходность данной бумаги.

Риск портфеля ценных бумаг определяется средним квадратическим отклонением доходности портфеля:

, где , 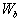— процентные доли данных бумаг в портфеле; , — риск данных бумаг (среднеквадратическое отклонение); —коэффициент линейной корреляции.

С использованием модели Марковица для расчета характеристик портфеля прямая задача приобретает вид:

Обратная задача представляется аналогичным образом:

При практическом применении модели Марковица для оптимизации фондового портфеля используются следующие формулы:

• доходность ценной бумаги:

, где Т – количество прошлых наблюдений доходности данной ценной бумаги.

• риск ценной бумаги (в виде оценки среднего квадратического отклонения):

3) статистическая оценка коэффициента корреляции между показателями доходности двух ценными бумагами:

,

где — доходность ценных бумаг a и b в период t.

Ясно, что для N рассматриваемых ценных бумаг необходимо рассчитать

коэффициентов корреляции.

Дата добавления: 2015-10-23