Интервальное прогнозирование по оцененной линейной эконометрической модели парной регрессии значений эндогенной переменной

Рассмотрим дробь 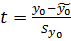, где 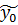- прогнозное значение. Эта дробь имеет смысл нормированно ошибки прогноза и называется дробью Стъюдента. Заметим, что эта величина является случайной переменной (СП). При справедливости сделанных предположений о случайном возмущении модели дробь Стьюдента обладает известным законом распределения (ЗР) – распределением Стьюдента (или t-распределением) с числом степеней свободы 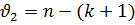, где (k+1) – количество оцениваемых коэффициентов модели.

Данное обстоятельство позволяет построить замкнутый интервал с границами, именуемый доверительным, который накрывает прогнозируемое значение 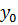эндогенной переменной с принятой доверительное вероятностью β. В последних двух выражениях символом t_крит обозначено критическое значение модуля дроби Стьюдента.

Обсужденная выше процедура интервального прогнозирования значений эндогенной переменной генерирует естественное правило объективной (формализованной) проверки адекватности оцененной модели:

1. Результаты наблюдений объекта-оригинала (выборку) разделить на два класса. В первый класс, именуемый обучающей выборкой, включить основной объем результатов наблюдения объекта-оригинала (90-95% выборки X, 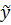. Оставшиеся результаты наблюдений (например, пара (x₀,y₀)) составляют контролирующую выборку.

2. По обучающей выборке оценить МНК-модель.

3. Задаться доверительной вероятностью β и по значениям регрессоров, входящих в контролирующую выборку (например, по значению x₀), построить доверительные интервалы для соответствующих этим регрессорам значений эндогенной переменной модели (например, y₀).

4. Проверить, попадают ли значения эндогенной переменной из контролирующей выборки (например, значение y₀) в соответствующие доверительные интервалы (например, в интервал . Если да, то признать оцененную модель адекватной; если же нет, то оцененная модель не может быть признана адекватной и подлежит доработке.

Процедуры интервального прогнозирования и проверки адекватности модели требуют значений t_крит. Чем выше значимость прогнозов, тем большее значение доверительное вероятности приходится принимать.

Дата добавления: 2015-10-23