Начнем с проблемы идентификации уравнений модели.

Суть проблемы рассмотрим на примере элементарной модели конкурентного рынка.

Для упрощения понимания оставим в модели только ее поведенческую часть. Структурная форма этой модели имеет вид:

(9.1)

Модель (9.1) содержит четыре неизвестных параметра: – это коэффициенты первых двух поведенческих уравнений модели. Заметим, что в третьем уравнении, тождестве, неизвестных параметров нет.

Оценки перечисленных параметров требуется вычислить по результатам наблюдений за переменными . Модель (9.1) закрытая, все ее текущие переменные эндогенные.

Реально для наблюдения доступны только две величины: равновесная цена и соответствующие этой цене уровни спроса и предложения, которые в соответствии с третьим уравнением модели (9.1) равны между собой.

Запишем модель (9.1) в приведенной форме:

(9.2)

Здесь - значение равновесной цены, а 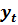- значение одновременно уровней спроса и предложения. Система уравнений (9.2) представляет собой систему двух уравнений с четырьмя неизвестными. Известно, что такая система не обладает единственностью решения. Более того, конкретно система (9.2) имеет бесконечное множество решений.

Графически эту ситуацию можно проиллюстрировать следующим образом.

Графики спроса и предложения образуют на плоскости с координатами известный крест Маршала, пересечение которого соответствует равновесной цене рис. 9.1.

На рис. 9.1. - значение равновесной цены, а - соответствующий ей уровень спроса и предложения.

Рис. 9.1. График модели конкурентного рынка.

Наблюдению поддается только точка Е₀. Мы пытаемся через эту одну точку провести две прямые. Очевидно, что однозначно это сделать невозможно. Для построения прямой необходимо иметь две точки, ей принадлежащие.

Казалось, что с учетом случайных возмущений, которые присутствуют в поведенческих уравнения модели, появится возможность решить эту проблему. Однако, это не так. Учет случайных возмущений только превращает точку Е₀ в «пятно», но никак не позволяет идентифицировать ни одну из прямых.

Вопрос. Как изменить спецификацию модели, чтобы она стала идентифицируемой, а наблюдаемые значения переменных объекта содержали достаточную информацию для однозначной оценки параметров структурной формы модели?

Для ответа на этот вопрос рассмотрим спецификацию модели конкурентного рынка, учитывающую влияние располагаемого дохода на уровень спроса. Спецификация такой модели имеет вид:

(9.3)

Здесь x_t располагаемый доход потребителя. В спецификации (9.3) также опущены случайные возмущения для облегчения интерпретации модели.

Очевидно, что при различном располагаемом доходе потребитель может приобрести продукт по разной цене. Это, в свою очередь, инициирует перемещение графика спроса вдоль оси p_t. Графически эта ситуация будет выглядеть так (Рис. 9.2):

Рис. 9.2. График модели конкурентного рынка с учетом располагаемого дохода потребителя.

Первый потребитель с небольшим доходом х₁ приобрел товар по более низкой цене, соответствующей спросу 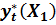и определил положение точки Е₁ на графике спроса. Второй потребитель с более высоким доходом позволил себе приобрести товар по более высокой цене, что дало возможность зафиксировать точку Е₂ на графике спроса. Учитывая, что график уровня предложения в обоих случаях оставался неизменным, получается возможность однозначно его определить, проведя прямую через точки Е₁ и Е₂. Заметим, что идентифицировать функцию предложения модели (9.2) удалось по наблюдениям за теми же двумя переменными: , и дополнительно за переменной Х_t. Переменные являются текущими эндогенными переменными, а переменная X_t экзогенная переменная.

Вывод. По результатам наблюдений за тройкой переменных удалось идентифицировать функцию предложения. Однако функция спроса осталась по-прежнему неидентифицируемой!

Но теперь можно сформулировать правило преобразования спецификации уравнений модели из неидентифицируемого вида к идентифицируемому. Для того, чтобы сделать модель предложения идентифицируемой была добавлена дополнительная экзогенная (предопределенная) переменная в уравнение спроса. Отсюда правило: чтобы сделать идентифицированным уравнение модели, необходимо ввести дополнительную предопределенную переменную в уравнение смежное с неидентифицируемым.

В качестве таких переменных часто используются лаговые эндогенные переменные. В рассматриваемом примере, чтобы сделать уравнение спроса идентифицируемым можно добавить во второе уравнение модели лаговое значение равновесной цены. Тогда все уравнения модели

(9.4)

будут идентифицируемыми.

Итак, методика устранения неидентифицируемости уравнений в системе линейных одновременных уравнений заключается в целенаправленном включении в уравнения модели предопределенных переменных. При этом, дополнительные переменные включаются в уравнение смежное с неидентифицируемым.

Остается вопрос. Как определить в системе линейных одновременных уравнений, какие из них идентифицируемые, а какие нет?

Для ответа на этот вопрос пользуются двумя теоремами. Одна из них (правило ранга) формулирует необходимое и достаточное условие идентифицируемости уравнения модели, другая (правило порядка) – необходимое условие идентифицируемости.

Дата добавления: 2015-10-29