Запись уравнения Шредингера для кет-вектора и уравнение нормировки в обозначениях П.Дирака

Пусть - волновая функция (функция состояния) обладающая полнотой информации о системе, удовлетворяющая уравнению Шредингера; 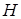-оператор Гамильтона, а - постоянная Планка. Функция состояния нормирована следующим образом:

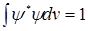, где , - функция состояния, и функция сопряженная ей, - элемент объема; интегрирование ведется по всему пространству существования волновой функции; обозначение *, звездочка означает комплексное сопряжение.

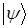Запись нормировки функции состояния , упрощается при введении обозначений «бра» и «кет», введенных П.Дираком. Вектор состояния обозначается и называется кет-вектором. Бра-вектор обозначается как , а произведение бра - и кет представляет собой интеграл .

Произведение любых бра – векторов и кет– векторов представляет собой скалярное произведение, равное . Скалярное произведение обладает свойствами: ,

В обозначениях П.Дирака запись уравнения Шредингера для кет-вектора и уравнение нормировки имеют вид:

, .

Дата добавления: 2015-09-02