Свойство антисимметричности волновых функций.

Волновая функция системы частиц с полуцелым спином (в частности, электронов) должна быть антисимметрична относительно перестановки координат любых двух частиц:

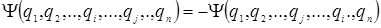
Антисимметрия волновой функции электронов была постулирована В. Паули

1.19. Решение волнового уравнения для свободного электрона с энергией 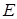и массой .

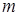Волновая функция является непрерывной, имеет непрерывные производные и удовлетворяет линейному дифференциальному уравнению эллиптического типа второго порядка.

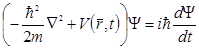, Если потенциальная энергия не зависит от времени, то решение можно искать в виде 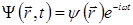. С учетом того, что энергия частицы 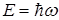, уравнение принимает вид:

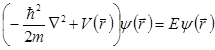, Свободно движущийся электрон с энергией 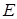и массой 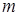. Потенциальная энергия 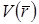в этом случае равна нулю, вследствие чего 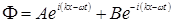, Где

Таким образом, свободный электрон описывается некоторой плоской волной, которая обладает энергией и импульсом .В общем случае предполагается, что электрон движется вдоль оси 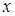слева направо, при этом коэффициент 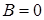. Тогда движение свободного электрона приобретает вид: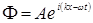

1.20. Решение уравнения Шрёдингера для атома водорода с кулоновским потенциалом взаимодействия .

Решение уравнения Шрёдингера получено для атома водорода с кулоновским потенциалом взаимодействия , т.е. при потенциале взаимодействия обратно пропорциональном расстоянию между протоном и электроном.

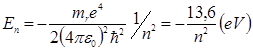
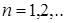Где 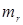- приведенная масса системы протон-электрон.

В физике твердого тела используется модель гармонического осциллятора Разрешенные энергетические уровни имеют вид: ,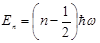

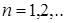
1. Матричная формулировка квантовой теории.

Постулаты квантовой теории и ее физи­ческая интерпретация основаны на волновой функции 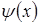и действующих на эту функцию линейных операторов, которые в общем случае являются комбинациями функций от 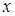и 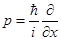. Матричная формулировка квантовой механики впервые предложена Гейзенбергом, в рамках этого подхода операторы выражаются матрицами. Преимущество матричной формулировки заключается в ее большей общности, а недо­статок — большие трудности при применениях для решения специаль­ных сложных задач, таких, например, как задача по определению стационарных состояний атомов.

Дата добавления: 2015-09-02