Диагональные матрицы. Единичная матрица.Обратная матрица.

Матрица 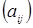, у которой все элементы равны нулю, за исключением элементов с равными индексами , называется диагональной матрицей. В квадратной таблице она.выглядит следующим образом:

Диагональную матрицу всегда можно записать в виде

, где — символ Кронекера, равный нулю при и единице при .

Единичная матрица. Частным случаем диагональной матрицы является единичная матрица, у которой все диагональные элементы равны единице. Поэтому она имеет вид .

Единичная матрица часто обозначается символом (. Умножение единичной матрицы на произвольную матрицу дает ту же самую матрицу

Обратная матрица. Во многих случаях можно определить обратную матрицу, которая аналогична обратной величине числа. Матрица , обратная матрице А, имеет следующее свойство:

Отметим, что по определению каждая матрица коммутирует со своей обратной матрицей (если последняя существует). Чтобы получить матрицу, обратную данной, положим и

Тогда мы должны иметь , Это уравнение можно рассматривать как систему неоднородных линейных уравнений, определяющих by через . Решая эти уравнения, запишем

где - детерминант, образованный из элементов , а минор этого детерминанта. Необходимым и достаточным условием существования обратной матрицы является отличие от нуля детерминанта .

Дата добавления: 2015-09-02