Нестационарное уравнение Шредингера в операторной форме.

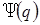Волновую функцию можно представить тогда в виде произведения координатной и временной частей: (1.25)

Подставляя (1.25) в (1.24) и разделяя переменные, получим (1.26)

Левая часть уравнения (1.26) не зависит от времени, а правая — от координат, вследствие чего каждая из частей должна быть равна конст Е, которая определяет полною энергию системы: (1.27) 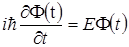(1.28) нестационарное ур-е шредингера

1.9 Уравнение Шрёдингера для стационарного состояния.

Функция состояния должна удовлетворять уравнению

(1-24)

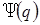Волновую функцию можно представить в виде произведения координатной и временной частей: (1.25), Подставляя (1.25) в (1.24) и разделяя переменные, получим (1.26). Левая часть уравнения (1.26) не зависит от времени, а правая — от координат, вследствие чего каждая из частей должна быть равна конст Е, которая определяет полною энергию системы: (1.27) (1.28)

Выражение (1.27- уравнением Шрёдингера для стационарного состояния). Это линейное дифференциальное уравнение второго порядка в частных производных эллиптического типа. Функция 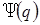является собственной функцией оператора Н, а Е — собственным значением. Из теории уравнений типа (1.27) известно, что линейный самосопряженный оператор, каким и является Н, всегда имеет полную систему собственных функций. Каждому собственному значению 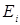соответствует собственная функция .

Дата добавления: 2015-09-02