Оператор координаты. Оператор импульса.

Оператор импульса 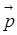выражается через операторы проекций, например на декартовы оси координат:

(1.12), 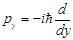(1.13), 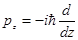(1.14)

Так, например, 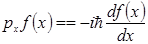(1.15)

Функция от любых динамических переменных f(p,q) заменяется на оператор f (p, q), который получается из классического выражения этой функции заменой р и q:на отвечающие им операторы р и q f(p,q)= f( p,q ) (1.16)

Потенциальная энергия V=V(q, t) есть функция только координат и времени, вследствие чего оператор V выражается через операторы координат по тем же формулам, что и потенциальная энергия в классической механике, т. е. V= V(q, t). (1.22)

Из правил построения операторов динамических переменных видно, что квантовая механика принципиально нуждается в классической для своего построения и обоснования.

Рассмотрим, для каких операторов квантовой механики выпол­няется условие (1.9), т. е. какие операторы коммутируют между собой. Заметим, что [х, у] = 0; [р*, pj=0 и т. д.

Операторы импульса р и координаты г не являются коммутиру­ющими. Легко проверить, что для них выполняются соотнош (1.23) ; ;

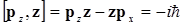Отметим, что две физические величины могут быть одновремен­но измерены только в том случае, если их операторы коммутируют между собой (доказательство этого утверждения см. на с. 16). Отсутствие коммутации операторов риг между собой и отражает то обстоятельство, что координата и импульс одной и той же частицы не могут быть одновременно измерены с любой наперед заданной степенью точности.

Дата добавления: 2015-09-02