Полная система функций. Собственными функциями и собственные числа.

Система функций 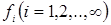называется полной, если любую функцию g можно разложить в ряд по функциям , где 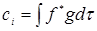. Если при этом выполняется условие 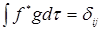для любых 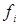и 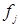из этой системы, то она называется ортонормированной.

Аналогично, для любого оператора 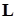функции и числа 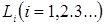удовлетворяющие уравнению:

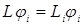называют соответственно собственными функциями и собственными числами оператора 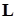. Если 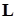— самосопряженный (эрмитов) опера­тор, то для него, так же как и для 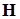, справедливы все вышеприведенные утверждения: система функций , является полной; и 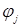соответствующие различным собственным числам и 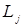, ортогональны. Если есть два различных оператора и , то собственные функции одного оператора отличны от собственных функций другого оператора. Но имеется весьма важное исключение из этого правила, которое приводится без доказательства: если два оператора и коммутируют между собой, т. е. 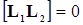, то можно выбрать систему базисных функций так, чтобы они являлись собственными функциями как так и . Таким образом, если какой-либо оператор 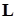коммутирует с 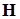, то система волновых функций , оператора 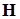будет также системой собственных функций оператора .

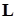Дата добавления: 2015-09-02