Определение бра -вектора через кет-вектор.

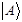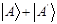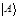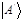При определении в математической теории некоторой совокупности векторов, почти всегда возможно введение дуальной последовательности векторов. Пусть каждому кет-вектору соответствует число , которое является функцией кет-вектора. Предположим что эта функция линейна и число соответствующее сумме кет-векторов есть сумма чисел соответствующих и . Число соответствующее 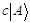, есть число соответствующее 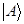, умноженное на численный множитель 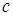. Тогда число , соответствующее любому , можно рассматривать как скалярное произведение кет-вектора на новый вектор, при этом каждой линейной функции от 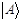соответствует один из новых векторов.

Для обозначения этих новых векторов вводится символ 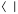, а сами векторы называются бра-векторами. Скалярное произведение бра-вектора 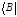на кет-вектор 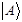для краткости записывается в виде: . Символы 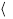и рассматриваются как скобки особого вида. Тогда скалярное произведение 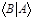представляет собой полное скобочное выражение, а кет-вектор 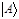и бра-вектор 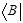- неполные скобочные выражения.

Символическая запись 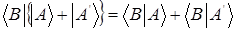(4)

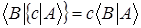, (5) где с любое число, означает, что скалярное произведения векторов и 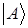есть линейная функция от 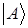. Бра-вектор определен полностью, если задано его скалярное произведение с любым кет-вектором.

Дата добавления: 2015-09-02