Определение суммы бра-векторов.

Сумма двух бра-векторов и определяется из условия, чтобы скалярное произведение суммы на кет-вектор 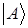было равно сумме скалярных произведений и на . (6)

2.12 Скалярное произведение векторов и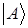

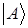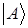Сумма двух бра-векторов и определяется из условия, чтобы скалярное произведение суммы на кет-вектор было равно сумме скалярных произв и на . (6)

Произв бра-вектора на число с определяется из условия: . (7) Из уравнений (2) и (5) следует, что произведение бра-вектора и кет-вектора удовлетворяет дистрибутивному закону умножения, а уравнения (3) и (6) показывают, что умножение кет-векторов на численные множители удовлетворяют обычным алгебраическим аксиомам.

Пусть между кет-вектором и соответствующим бра-вектором существует взаимно-однозначное соответствие такое, что бра, соответствующий сумме , есть сумма бра, соответствующих 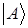и , а бра, соответствующий 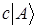. равен бра, соответствующему 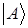, умноженному на , где - число, комплексно-сопряженное числу 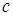. Для образования соответствующих векторов используется то же обозначение, так бра-вектор, соответствующий кет-вектору 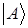обозначается, как .

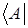Существование скалярного произведения бра-вектора и кет-вектора и позволяет установить между ними соотношение сопряженности. Бра- и кет-векторы являются комплексными величинами, их можно умножать на комплексные числа и после чего их природа не меняется, однако они являются комплексными величинами особого рода, т.к. их нельзя разбить на вещественную и мнимую часть. Бра-векторы и кет- векторы нельзя складывать.

Произведение любых бра – векторов и кет– векторов представляет собой скалярное произведение, равное . Скалярное произведение обладает свойствами: ,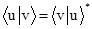

2.13 2.14 Длина бра-вектора и Длина кет-вектора

Длина бра-вектора 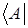или сопряженного кет-вектора 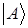определяется как квадратный корень из положительного числа . Если состояние системы характеризуется бра- или кет-вектором, то будет определено только направление вектора – сам вектор определяется только направление вектора, сам вектор будет определен с точностью до постоянного произвольного множителя. Этот множитель выбирается так, чтобы длина вектора была единичной. Процедура выбора множителя называется нормировкой, а выбранный таким образом вектор – нормированным.

Дата добавления: 2015-09-02