Собственные функции и собственные операторы.

уравнение Шрёдингера для стационарного состояния. Это линейное дифференциальное уравнение второго порядка в частных производных эллиптического типа. Функция 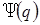является собственной функцией оператора Н, а Е — собственным значением. Из теории уравнений типа (1.27) известно, что линейный самосопряженный оператор, каким и является Н, всегда имеет полную систему собственных функций. Каждому собственному значению 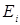соответствует собственная функция .

Если одно собственное значение соответствует одновременно нескольким собственным функциям , то состояние называется вырожденным с кратностью вырождения, равной т. Любая линейная комбинация функций, соответствующих вырожденному состоянию, также будет удовлетворять уравнению (I.27) с тем же самым собственным числом 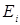.Функции , и относящиеся к различным собственным значе­ниям Ei и E_h ортогональны, т. е. выполняются соотношения: (1.29)

Дата добавления: 2015-09-02