Матричное представление оператора.

Для того, чтобы записать oneратор в матричном представлении, рассмотрим сначала некоторую волновую функцию 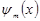, которая входит в совокупность полной ортонормированной системы волновых функций . В частном 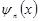может быть , если мы рассматриваем ортонормированную систему гармонических функций, или же 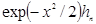, где h_n — полином Эрмита — Чебышева.

Рассмотрим новую волновую функцию , полученную действием оператора на , т. е.

(1), Так как образует полную ортонормированную систему, то воз­можно разложить функцию в ряд по :

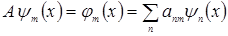
Если числа а_пт известны для всех т и п, то действие оператора на любую волновую функцию 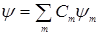можно представить следующим образом

Если оператор задан, то для того чтобы определить коэффициенты разложения

нужно умножить выражение (1) на и проинтегрировать по всем 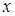. Поскольку функции образуют ортонормированную систему, то можно записать выражение для любого :

Коэффициенты а_пт, в общем случае являющиеся комплексными, образуют

прямоугольную таблицу чисел, которая схематически имеет вид:

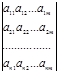
Можно показать, что совокупность чисел а_тп обладает всеми свой­ствами таких величин,

которые называются в математике матрицами. Каждое число а_тп называется элементом (или компонентой) ма­трицы. Для обозначения всей суммы матричных элементов часто используется символ А, ее также выражают в виде (а_тп).

Дата добавления: 2015-09-02