Суперпозиция состояний в записи Дирака.

Единичная матрица превращается в -функцию Дирака диагональная матрица принимает вид . Можно вывести также следующее правило умножения непрерывных матриц: 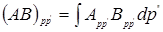Математическая формулировка принципа суперпозиции состояний квантовых систем.

2.9. Образование кет-вектора из векторов 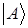и

Состояния системы в квантовой механике связываются с векторами, определенными в Гильбертовом пространстве. Вектор, с которым сопоставляется состояние системы носит название кет-вектора, или просто кет и обозначается символом . Кет-векторы в общем случае определены в бесконечномерном пространстве, и обозначаются буквой, например 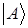. Кет-векторы можно умножать на комплексные числа и складывать между собой. Приведенная формула показывает, каким образом из двух кет-векторов 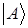и образуется новый кет-вектор. 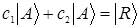(1). где - комплексные числа.

Дата добавления: 2015-09-02