Все реальные газы с уменьшением плотности приближаются по своим свойствам к идеальным газам, поэтому уравнение Ван-дер-Ваальса при переходит в уравнение Менделеева - Клапейрона.

Раскрыв скобки в уравнении (3) и умножив на 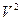, получаем

(4)

Мы получили кубическое уравнение относительно , коэффициенты которого зависят от параметров .

В зависимости от соотношения между коэффициентами решения уравнения могут быть либо все три вещественными, либо одно вещественное и два комплексных, не имеющих физического смысла.

На рис.6.5 изображены изотермы Ван-дер-Ваальса для нескольких значений температуры.

При температуре и давлении в пределах от до коэффициенты в (4) таковы, что все три решения вещественные; при других коэффициентах уравнение имеет только одно вещественное решение.

Различие между тремя вещественными решениями с ростом температуры уменьшается (ср. изотермы и , > ).

Начиная с определенной, своей для каждого вещества температуры вещественным остается только одно решение уравнения (4). Температура , называемая критической.

Если повышать температуру, то точки, соответствующие решениям уравнения , , все больше сближаются, сливаясь при критической температуре в одну точку (на рис. Точка К).

Точка К называется к ритической. Ей соответствуют три совпадающих вещественных решения уравнения (4). Касательная к критической изотерме в точке К является пределом, к которым стремятся секущие и и т.д. при приближении температуры к критической. Следовательно, эта касательная, ак и все секущие, параллельна оси V, так, что производная 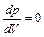в точке К. Кроме того в точке перегиба должна быть равна нулю и вторая производная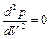

Из уравнения (1) выразим давление:

Продифференцируем это уравнение по :

В критической точке при эти выражения должны обращаться в ноль:

Для критической точки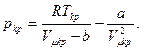

Мы получили систему из трех уравнений с неизвестными .

Решение этой системы имеет вид

Таким образом, зная константы Ван-дер-Ваальса и, можно найти соответствующие критической точке , которые называются критическими величинами. И, наоборот, по известным критическим величинам могут быть найдены значения констант Ван-де- Ваальса.

Для критических величин , в то время как

согласно уравнению Менделеева - Клапейрона для идеального газа .

Дата добавления: 2015-08-21