Эта константа равна учетверенному объему молекул.

Докажем, что поправка b в 4 раза больше собственного объема всех N _А молекул одного моля газа:

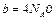(6.9)

Для доказательства рассмотрим сферу радиуса d, центр которой совпадает с центром произвольной молекулы.

· Внутри этой сферы не могут находиться центры других молекул.

· Объем этой сферы является «запрещенным» объемом для центров всех молекул, соударяющихся с данной.

· Поскольку молекулы сталкиваются попарно (вероятность столкновений трех и более молекул мала), приведенное рассуждение справедливо для любой пары молекул. Таким образом, в расчете на каждую из молекул газа недоступным будет объем, равный четырем объёмам одной молекулы, а для всех молекул – объем равный учетверенному суммарному объему молекул. Он в восемь раз больше собственного объема молекулы.

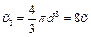
Поправка Ван-дер-Ваальса b представляет собой «запрещенный» объем, приходящийся на все N_A молекул, т.е.

,

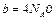что и требовалось доказать.

Из формулы (6.9)следует: значение b зависит от эффективного диаметра молекул, т. е. от химической природы газа.

2. Поправка ,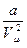

- обусловлена силами притяжения между молекулами.

- имеет размерность давления,

- и ее часто называют внутренним давлением.

Несколько сложнее учесть влияние сил взаимного притяжения молекул, которые очень быстро убывают с увеличением расстояния между молекулами.

Поэтому можно считать, что каждая молекула взаимодействует лишь с теми молекулами, которые находятся от нее на расстояниях ,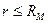

где R_M — радиус молекулярного действия, имеющий значение порядка 10 ^-9 м.

Сферу радиуса R_M, построенную вокруг молекулы, называют сферой ее молекулярного действия.

· Если молекула находится вдали от стенок сосуда, то вся сфера ее молекулярного действия заполнена другими молекулами, так что результирующая сила притяжения для рассматриваемой молекулы равна нулю.

· Если молекулы, находятся вблизи стенки MN сосуда (рис. 6.3).

У них сферы молекулярного действия только частично находятся внутри газа (области, закрашенные на рис. 6.3).

Найдем равнодействующую сил притяжения, приложенных к произвольной молекуле К, находящейся в слое газа, пограничном со стенкой.

Для этого разобьем сферу молекулярного действия молекулы К на четыре области: а, б, г, д (рис. 6.4).

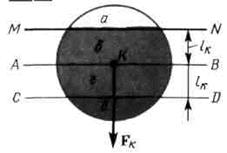- Плоскости АВ и CD проведены параллельно поверхности стенки MN,

- плоскость CD симметрична поверхности стенки относительно диаметральной плоскости АВ.

Области б, г, д заполнены молекулами газа, область а - нет.

Силы, действующие на молекулу К со стороны молекул, находящихся в шаровых слоях

- б, г, взаимно уравновешиваются.

- Притяжение же молекулы К частицами, находящимися в шаровом сегменте д, ничем не компенсируется, так как в сегменте а молекул газа нет.

Очевидно, что результирующая сила F_k должна быть

· направлена перпендикулярно стенке внутрь газа (рис. 6.4).

· сила пропорциональна концентрации молекул газа: 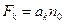(6.10)

где коэффициент 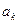зависит

- от химической природы газа,

- расстояния 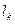от центра молекулы К до стенки сосуда.

Если 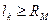, то области а, д исчезают и F_k = 0.

Таким образом, молекулы, отстоящие от стенок сосуда на расстояниях R_M и больших, уже можно считать «внутренними».

Действие сил F_k приводит к тому, что в пограничном со стенкой слое газа молекулы

· движутся по направлению к стенке замедленно.

· ведут себя подобно шарам, которые прикреплены к пружинам и растягивают их в процессе движения за счет убыли своей кинетической энергии.

Поэтому удары молекул о стенки несколько смягчены.

Давление, производимое на стенки реальным газом, меньше, чем в случае идеального газа р_ид., имеющего ту же температуру Т и ту же концентрацию:

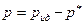(6.11),

где р*— давление, обусловленное действием сил взаимного притяжения молекул (внутреннее давление).

Внутри газа силы взаимного притяжения молекул не влияют на их движение, и давление газа равно р_ид.

У стенок оно меньше этого давления и равно р.

Добавочное давление р* производит на газ слой его молекул, граничащих со стенками.

Оно вызвано силами F_k и равно

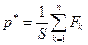(6.12)

где сумма сил Fк распространена на все n молекул пограничного слоя газа,

S — площадь стенок сосуда.

Заменив F_k по формуле (6.10), получим

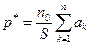или 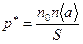(6.13),

где 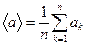- среднее значение коэффициента 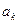для всех молекул пограничного слоя, зависящее только от химической природы газа.

- число молекул, заключенных в пограничном слое,

Подставив это выражение в (6.13), получим

(6.14),

Где

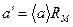(6.15),

Из уравнений (6.14) и (6.15) имеем

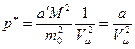(6.16),

Коэффициент Ван-дер-Ваальса 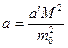зависит только от химической природы газа

Из (6.16) и (6.11) получим выражение для давления внутри газа:

где р — давление газа на стенки сосуда.

Подставив в уравнение Клапейрона — Менделеева ()вместо и р_ид вместо р, получим уравнение состояния реальных газов, которое было выведено нидерландским физиком Я. Д- Ван-Дер-Ваальсом (1873) и названо его именем:

В результате уравнение состояния одного моля реального газа приняло вид

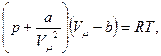(1) - уравнение Ван-дер-Ваальса.

Здесь а и b — постоянные Ван-дер-Ваальса, для разных газов они имеют свои значения.

Если мы имеем дело не с одним, а с 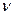молями газа объемом V, то в уравнении (1) следует сделать замену:

.

Газ, подчиняющийся уравнению (1), называют ван-дер-ваальсовским.

Уравнение Ван-дер-Ваальса при большой простоте дает возможность качественно объяснить широкий круг явлений в газах и в жидкостях.

Пример: Найдем давление, при котором плотность углекислого газа с температурой Т= 300 К равна 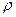= 500 г/л.

Считая газ ван-дер-ваальсовским, представим (1) в виде

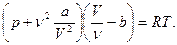(2)

Подставив и 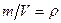, получим:

.

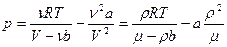Для углекислого газа а = 0,367 Па·м /моль, b = 4,3·10 м /моль и = 44 г/моль. В результате подстановки найдем р 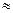80 атм. Расчет же по формуле состояния идеального газа дает 280 атм. Различие весьма значительное.

Дата добавления: 2015-08-21